Multiple Zeta Functions, Multiple Polylogarithms And Their Special Values

Jianqiang Zhao

• Publisher: WSPC
• Year: 2016
• eBook ISBN: 9789814689410
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

This is the first introductory book on multiple zeta functions and multiple polylogarithms which are the generalizations of the Riemann zeta function and the classical polylogarithms, respectively, to the multiple variable setting. It contains all the basic concepts and the important properties of these functions and their special values. This book is aimed at graduate students, mathematicians and physicists who are interested in this current active area of research.

The book will provide a detailed and comprehensive introduction to these objects, their fascinating properties and interesting relations to other mathematical subjects, and various generalizations such as their q -analogs and their finite versions (by taking partial sums modulo suitable prime powers). Historical notes and exercises are provided at the end of each chapter.

Contents:

• Multiple Zeta Functions
• Multiple Polylogarithms (MPLs)
• Multiple Zeta Values (MZVs)
• Drinfeld Associator and Single-Valued MZVs
• Multiple Zeta Value Identities
• Symmetrized Multiple Zeta Values (SMZVs)
• Multiple Harmonic Sums (MHSs) and Alternating Version
• Finite Multiple Zeta Values and Finite Euler Sums
• q -Analogs of Multiple Harmonic (Star) Sums

Readership: Advanced undergraduates and graduate students in mathematics, mathematicians interested in multiple zeta values.
Zeta Functions;Polylogarithms;Multiple Zeta Functions;Multiple Zeta Values;Multiple Polylogarithms;Multiple Harmonic Sums;Double Shuffle Relations;Mixed Hodge Structures;Drinfeld Associator;Quasi-symmetric Functions;Regularizations;q-analogs Key Features:

• For the first time, a detailed explanation of the theory of multiple zeta values is given in book form along with numerous illustrations in explicit examples
• The book provides for the first time a comprehensive introduction to multiple polylogarithms and their special values at roots of unity, from the basic definitions to the more advanced topics in current active research
• The book contains a few quite intriguing results relating the special values of multiple zeta functions and multiple polylogarithms to other branches of mathematics and physics, such as knot theory and the theory of motives
• Many exercises contain supplementary materials which deepens the reader's understanding of the main text

Chapter 1

Multiple Zeta Functions

The multiple zeta functions are nested generalizations of the Riemann zeta function. In this chapter we start by summarizing briefly the most important results of the Riemann zeta function. Then we bring in one of our major players in this book — the multiple zeta function — and outline its main properties and problems. Some results will be generalized to higher levels in Chap. 13, but often with more advanced and different proofs. So, we still provide complete proofs of these results in this chapter.

1.1Riemann Zeta Function

There are numerous accounts in the literature about the Riemann zeta function defined as follows:

As motivations for further generalizations, we list some of its most important properties below.

•Euler product formula. For Re(s) > 1,

•The functional equation. The Riemann zeta function can be analytically continued to a meromorphic function on the whole complex s-plane, which is holomorphic everywhere except for a simple pole at s = 1 with residue 1. Moreover, it satisfies

•Special values. For any positive even number 2n,

where B_2n are Bernoulli numbers defined by the generating function

For negative integers −n < 0, one has

•Generating function of the special values. Let

be the digamma function defined for all x unequal to a negative integer. Then for all |x| < 1

where γ ≈ 0.57721566 . . . is Euler’s constant. See, for example, [6, §6.3]. Moreover, ψ satisfies the reflection, recurrence and duplication relations

and it has an important integral expression

•Zeros, the critical line, and the Riemann hypothesis. From Eq. (1.4) we see that ζ(s) has zeros at negative even integers (called trivial zeros). In his landmark 1859 paper [483] Riemann conjectured that all non-trivial zeros of ζ(s) must lie on the critical line Re(s) = 1/2. This is the famous “Riemann hypothesis”.

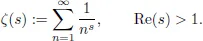
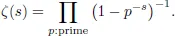
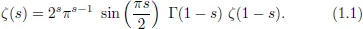
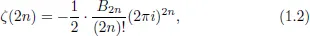
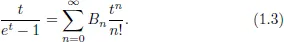
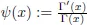
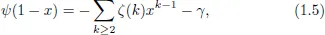
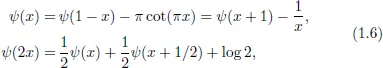
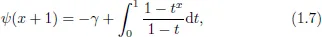
1.2Multiple Zeta Functions

The multiple zeta functions are multiple variable generalizations of the Riemann zeta function.

Definition 1.2.1. For fixed positive integer d and d-tuple of complex variables s = (s₁, . . . , s_d), the multiple zeta function is defined by

To guarantee convergence, s must satisfy Re(s₁ + · · · + s_j) > j for all j = 1, . . . , d where Re(s) is the real part of a complex number s (see Exercise 1.4). The number d is called the depth, denoted by dp(s). When all the variables are positive integers we call |s| := s₁ + · · · + s_d the weight. Furthermore, the multiple zeta star function is defined by

Remark 1.2.2. (i) In the literature the order 0 < k₁ < · · · < k_d is used sometimes, which gives rise to ζ(s_d, . . . , s₁) in our notation.

(ii) It is not hard to see that ζ*(s) can be expressed using the multiple zeta functions of different depths:

where

is either “+” or “,”. So we will consider only the multiple zeta functions in the rest of this chapter.

Similar to the Riemann zeta function one can study both the algebraic theory of the special values of the multiple zeta functions at positive integers, called the multiple zeta values and the analytic theory of the multiple zeta functions. In this chapter we will consider mainly the analytic side and postpone the treatment of the multiple zeta values to Chaps. 3–6.

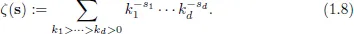
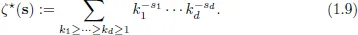
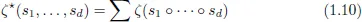
1.3Analytic Continuation

Since the multiple zeta function of depth d in Eq. (1.8) is defined only for complex arguments with certain restrictions it is essential to continue it analytically to the whole d-dimensional complex space in order to study special values at arbitrary integer arguments.

Recall that the Bernoulli polynomials B_k(x) are defined by the generating function

and the “periodic Bernoulli pol...

Table of contents

• Cover
• Halftitle
• Series Editors
• Title
• Copyright
• Dedication
• Contents
• Preface
• Introduction
• 1. Multiple Zeta Functions
• 2. Multiple Polylogarithms (MPLs)
• 3. Multiple Zeta Values (MZVs)
• 4. Drinfeld Associator and Single-Valued MZVs
• 5. Multiple Zeta Value Identities
• 6. Symmetrized Multiple Zeta Values (SMZVs)
• 7. Multiple Harmonic Sums (MHSs) and Alternating Version
• 8. Finite Multiple Zeta Values and Finite Euler Sums
• 9. q-Analogs of Multiple Harmonic (Star) Sums
• 10. Multiple Zeta Star Values (MZ*Vs)
• 11. q-Analogs of Multiple Zeta Functions
• 12. q-Analogs of Multiple Zeta (Star) Values
• 13. Colored Multiple Zeta Values
• 14. Colored Multiple Zeta Values at Lower Levels
• 15. Application to Feynman Integrals
• Appendix A Key Concepts of Hopf Algebras
• Appendix B Some Useful Results from Lie Algebras
• Appendix C Basics of Hypergeometric Functions
• Appendix D Sample Computer Codes
• Appendix E Tables of Special Values
• Appendix F Answers to Some Exercises
• Bibliography
• List of Abbreviations
• List of Symbols
• Index