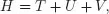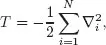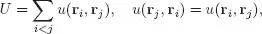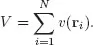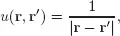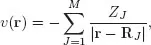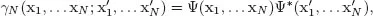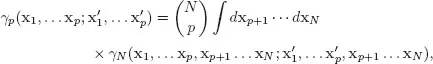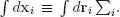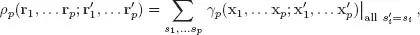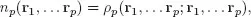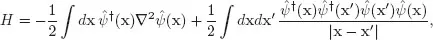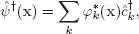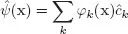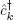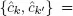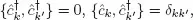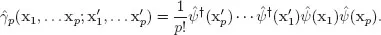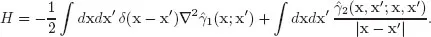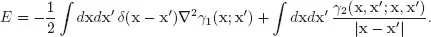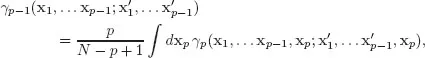Exactly Solvable Models In Many-body Theory

N H March, G G N Angilella

• Publisher: WSPC
• Year: 2016
• ISBN:
  9789813140165
• Topic: Naturwissenschaften
• Subtopic: Kondensierte Materie

The book reviews several theoretical, mostly exactly solvable, models for selected systems in condensed states of matter, including the solid, liquid, and disordered states, and for systems of few or many bodies, both with boson, fermion, or anyon statistics. Some attention is devoted to models for quantum liquids, including superconductors and superfluids. Open problems in relativistic fields and quantum gravity are also briefly reviewed.

The book ranges almost comprehensively, but concisely, across several fields of theoretical physics of matter at various degrees of correlation and at different energy scales, with relevance to molecular, solid-state, and liquid-state physics, as well as to phase transitions, particularly for quantum liquids. Mostly exactly solvable models are presented, with attention also to their numerical approximation and, of course, to their relevance for experiments.

Contents:

• Low-Order Density Matrices
• Solvable Models for Small Clusters of Fermions
• Small Clusters of Bosons
• Anyon Statistics with Models
• Superconductivity and Superfluidity
• Exact Results for an Isolated Impurity in a Solid
• Pair Potential and Many-Body Force Models for Liquids
• Anderson Localization in Disordered Systems
• Statistical Field Theory: Especially Models of Critical Exponents
• Relativistic Fields
• Towards Quantum Gravity
• Appendices

Readership: Graduate students and researchers in condensed matter theory.

Chapter 1

Low-order density matrices

1.1 Low-order spinless density matrix theory

We start by considering a generic assembly of N electrons, characterized by the Hamiltonian (in atomic units)

(1.1a)

(1.1b)

(1.1c)

(1.1d)

Here, as usual, T is the total kinetic energy operator, U denotes the electron-electron (e-e) repulsion energy operator, and V denotes the electron-nucleus (e-n) attraction energy operator, respectively. In realistic situations, one obviously has

(1.2a)

(1.2b)

(for a molecule, cluster, or solid characterized by M nuclei of charge Z_J, placed at fixed positions R_J, J = 1, . . . M), although the explicit functional form of u and v may be kept as indicated, in order to also embrace model systems.

The Nth-order density matrix (DM) associated with a normalized eigenfunction Ψ(x₁, . . . x_N) of the Schrödinger equation HΨ = EΨ is then defined as

(1.3)

where x_i = (r_i, s_i) is a shorthand notation for coordinates and spin variables of the ith electron. More generally, the pth-order reduced DM (pDM, with p < N) is defined by integrating out (N − p) coordinates as (see ter Haar, 1961; Holas and March, 1995, and references therein)

(1.4)

where, consistently with the above notation,

In cases where spin is not of interest, one considers a spin-averaged or spinless DM defined as

(1.5)

while the diagonal elements of the spinless DM are denoted by

(1.6)

with n_p ≥ 0. The basic quantity of interest in Density Functional Theory (DFT) is thus n(r) = n₁(r) = ρ₁(r; r), where the subscript ‘1’ can be omitted, for simplicity.

Expressing the Hamiltonian in second quantization as

(1.7)

where

(1.8a)

(1.8b)

are creation and annihilation quantum field operators at x, respectively, with

and ĉ_k fermion creation and annihilation operators,

in the single-particle spin-orbitals φ_k(x), the reduced pDM can be viewed as the quantum average of the operator

(1.9)

The same Hamiltonian can then be expressed in terms of 1DM and 2DM as

(1.10)

Similarly, the total (e.g. ground-state) energy of the system can be expressed as

(1.11)

This immediately generalizes also in presence of an external, one-body potential.

Moreover, since the Hamiltonian contains only (at most) 2-body interactions, and given the fact that a (p − 1)DM can be related to a pDM as

(1.12)

one can then express the total energy E as a functional of γ₂ alone, i.e. of its 2-bo...