An Introduction to Applied Matrix Analysis

Xiao Qing Jin, Seak-Weng Vong

• Publisher: WSPC
• Year: 2016
• eBook ISBN: 9789814749480
• Topic: Mathematics
• Subtopic: Algebra
• Index: Mathematics

It is well known that most problems in science and engineering eventually progress into matrix problems. This book gives an elementary introduction to applied matrix theory and it also includes some new results obtained in recent years.

The book consists of eight chapters. It includes perturbation and error analysis; the conjugate gradient method for solving linear systems; preconditioning techniques; and least squares algorithms based on orthogonal transformations, etc. The last two chapters include some latest development in the area. In Chap. 7, we construct optimal preconditioners for functions of matrices. More precisely, let f be a function of matrices. Given a matrix A, there are two choices of constructing optimal preconditioners for f ( A ). Properties of these preconditioners are studied for different functions. In Chap. 8, we study the Bottcher–Wenzel conjecture and discuss related problems.

This is a textbook for senior undergraduate or junior graduate students majoring in science and engineering. The material is accessible to students who, in various disciplines, have basic linear algebra, calculus, numerical analysis, and computing knowledge. The book is also useful to researchers in computational science who are interested in applied matrix theory.

Contents:

• Introduction and Review
• Norms and Perturbation Analysis
• Least Squares Problems
• Generalized Inverses
• Conjugate Gradient Method
• Optimal and Superoptimal Preconditioners
• Optimal Preconditioners for Functions of Matrices
• Böttcher–Wenzel Conjecture and Related Problems

Readership: Undergraduate students in linear and multilinear algebra/matrix theory, and numerical analysis.
Key Features:

• The preconditioning techniques proposed in Chapter 7 for matrix functions and an elementary proof of the Bottcher and Wenzel conjecture with related problems in Chapter 8 should be interesting to readers because they appear for the first time in a textbook

Chapter 1

Introduction and Review

We study and review several important topics in linear algebra [1; 6; 27; 43] which are essential for the development of later chapters.

1.1Basic symbols

We use the following symbols throughout this book.

•Let

denote the set of natural numbers,

denote the set of integers,

denote the set of real numbers,

denote the set of complex numbers, and

.

•Let

ⁿ denote the linear vector space of real n-vectors and

ⁿ denote the linear vector space of complex n-vectors. Vectors will almost always be column vectors.

•Let

^m×n denote the linear vector space of m×n real matrices and

^m×n denote the linear vector space of m × n complex matrices.

•The symbol 0 denotes the zero matrix or the zero vector with appropriate size.

•We use the upper case letters such as A, B, C, Δ, Λ, etc. to denote matrices. We use the bold lower case letters such as u, v, w, etc. to denote vectors, and use the lower case letters such as x, y, z, α, β, etc. to denote scalars.

•The symbol a_ij denotes the (i, j)th entry in a matrix A.

•For any matrix A, let A^T denote the transpose of A, A* denote the conjugate transp...

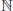
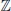
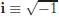
Table of contents

• Cover
• Halftitle
• Series
• Title Page
• Copyright
• Dedications
• Preface
• Contents
• 1. Introduction and Review
• 2. Norms and Perturbation Analysis
• 3. Least Squares Problems
• 4. Generalized Inverses
• 5. Conjugate Gradient Method
• 6. Optimal and Superoptimal Preconditioners
• 7. Optimal Preconditioners for Functions of Matrices
• 8. Böttcher-Wenzel Conjecture and Related Problems
• Bibliography
• Index