Book Of Numbers, The

Tianxin Cai, Jiu Ding

• Publisher: WSPC
• Year: 2016
• eBook ISBN: 9789814759458
• Topic: Sciences biologiques
• Subtopic: Science générale

Natural numbers are the oldest human inventions. This volume describes their nature, laws, history and current status. The first five chapters contain not only the basics of elementary number theory for the convenience of teaching and continuity of rea

Chapter VII

Additive and Multiplicative Number Theory

Additive number theory and multiplicative number theory are both important in number theory. Additive number theory is also called Dui Lei Su Shu Lun in Chinese by L.K. Hua (1910–1985), and he published a book with the title. As two branches of number theory, there are a few intersections between them. However, inspired by the form of the abc conjecture, we try to combine the addition and multiplication in Waring’s problem. We obtain a new class of Diophantine equations and some unexpected results. Later, this idea is gradually expanded, involving several classic number theory problems. Now we select six of them to study, including five classical number theory problems, and the last one is the abcd-equation, which is our creation. Recently, the Romanian-born Germany mathematician Preda Mihailescu published a survey article entitled Around ABC (Newsletter of European Math. Soc. 3 (2014) 29–35), and mentioned two of them. In a note he calls this kind of equations yin–yang equations.

31.New Waring’s Problem

In 1770, Lagrange showed (Section 17) that every positive integer can be expressed as a sum of at most four squares of nonnegative integers. The proposition was probably already known to Diophantus, since he gave some examples in his Arithmetic and later it was formally conjectured by the French mathematician and poet Bachet (1581–1638), who is the translator of the Latin version of Arithmetic (1621).

Portrait of English mathematician Waring

In his comments, Fermat claimed (as he did in Fermat’s last theorem) that he had proved this proposition, but no one found it. In the same year that Lagrange gave the proof, the English mathematician Edward Waring (1736–1798) asserted that for every k, there was a number s = s(k) such that every positive integer n can be expressed as a sum of s kth powers of positive integers, i.e.,

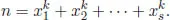
In the next 139 years, several special cases of Waring’s problem were solved, for example, k = 3, 4, 5, 6, 7, 8, 10. It was in 1909 that Hilbert finally solved the problem in the affirmative for all k. So Waring’s assertion is also called the Hilbert–Waring theorem. Once we know that...

Table of contents

• Cover
• Halftitle
• Title
• Copyright
• Preface
• Contents
• I. The Division Algorithm
• II. The Concept of Congruence
• III. Congruences
• IV. Quadratic Residues
• V. N th Power Residues
• VI. Congruences Modulo Integer Powers
• VII. Additive and Multiplicative Number Theory
• Appendix A The List of Prime Numbers Less Than 10000
• Bibliography