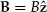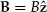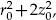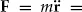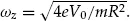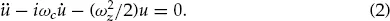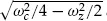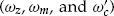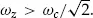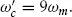Trapped Charged Particles

A Graduate Textbook with Problems and Solutions

Martina Knoop, Niels Madsen, Richard C Thompson

• Publisher: World Scientific Publishing Company
• eBook ISBN: 9781786340146
• Topic: Physical Sciences
• Subtopic: Atomic & Molecular Physics

At Les Houches in January 2015, experts in the field of charged particle trapping came together for the Second Winter School on Physics with Trapped Charged Particles. This textbook collates the lectures delivered there, covering the fundamental physics of particle traps and the different types of applications of these devices.

Taken as a whole, the book gives an overview of why traps for charged particles are important, how they work, their special features and limitations, and their application in areas such as precision measurements, mass spectrometry, optical clocks, plasma physics, antihydrogen creation, quantum simulation and quantum information processing. Chapters from various world experts include those on the basic properties of Penning traps and RF traps, as well as those covering important practical aspects such as vacuum systems, detection techniques, and different types of particle cooling, including laser cooling.

Each individual chapter provides information and guidance on the application of the above methods. Additionally, each chapter is complemented by fully worked problems and solutions, making Trapped Charged Particles perfect for advanced undergraduate and postgraduate students new to this topic.

Contents:

• Penning Traps
• Radiofrequency Traps
• The Guiding Center Approximation
• Toroidal Systems
• Ultrahigh Vacuum for Trapped Ions
• Laser Cooling Techniques Applicable to Trapped Ions
• Non-Laser Cooling Techniques
• Numerical Simulations of Ion Cloud Dynamics
• Plasmas in Penning Traps
• Plasma Modes
• Rotating Wall Technique and Centrifugal Separation
• Correlations in Trapped Plasma
• Autoresonance
• Antihydrogen Physics
• Ion Coulomb Crystals and Their Applications
• Cold Molecular Ions in Traps
• Precise Tests of Fundamental Symmetries with Trapped Ions
• Trapped-Ion Optical Frequency Standards

Readership: Advanced undergraduate and postgraduate students studying the field of trapped charged particles.
Key Features:

• The first textbook covering ion traps and their applications
• Written by world experts on each topic
• Includes worked exercises for each topic

CHAPTER ONE

PENNING TRAPS

Richard C. Thompson

Blackett Laboratory, Department of Physics,
Imperial College London, London SW7 2AZ, UK
[email protected].

Penning traps have been in use for a wide range of experiments in mass spectrometry, plasma physics, atomic spectroscopy, quantum information, and quantum optics for over 40 years. In this chapter, we give an account of the principles of operation of Penning traps, together with a discussion of practical aspects of their use and their advantages for particular types of experiments. A brief survey of recent experiments using Penning traps demonstrates their wide applicability and continuing importance in many fields.

1.Introduction

A Penning trap confines the motion of charged particles by the use of static electric and magnetic fields. In essence, a quadrupole electrostatic field confines particles along a particular direction (the axis of the trap) and the magnetic field, which is parallel to this axis, confines their motion perpendicular to the trap axis. In this way, the particles are trapped in all three dimensions. The Penning trap can be used for electrons, positrons, or atomic and molecular ions, including highly-charged ions. The principles of its operation are straightforward and it has found application in a very wide range of areas of physics.

We start this chapter with a brief historical introduction to Penning traps, then we discuss the operating principles of the trap (Section 2). In Section 3, we introduce a rotating frame in which the behavior of the trapped particles can be visualized in an intuitive manner. We then discuss the particular advantages and disadvantages associated with the Penning trap, and illustrate some of these advantages with brief discussions of some relevant experiments (Section 4). We then look at various practical aspects of the operation of the Penning trap (Section 5) including cooling techniques. In Section 6, we look in more detail at laser cooling in the Penning trap. Finally, we draw some overall conclusions about the Penning trap in Section 7.

The name “Penning Trap” was first introduced by Hans Dehmelt [1, 2] in the early 1960s. He later received the Nobel Prize for his work with ion traps [3]. The trap was named after Franz Penning, who performed experiments in the 1930s on electric discharges between coaxial cylinders and noticed that the lifetime of the electrons was increased in the presence of an axial magnetic field [4]. Dehmelt used the Penning trap for radiofrequency (RF) spectroscopy of He⁺ ions and demonstrated that the temperature of trapped ions could be measured by monitoring the induced current in an external circuit connected to the Penning trap electrodes (the so-called “Bolometric technique” [5]).

Other groups were also using Penning traps around the same time, for example, in Edinburgh, a Penning trap was used in the development of a source of polarized electrons [6]. In Mainz, measurements were made of the anomalous magnetic moment (i.e. the g-factor) of electrons in a trap [7, 8], and an impressive precision of around three parts in 10⁸ was obtained.

One of the most significant steps in the application of Penning traps in atomic physics was made in 1978 when laser cooling of trapped ions was first demonstrated [9]. This work also used the bolometric technique referred to above. Later experiments used fluorescence light for observing this process, as will be discussed later in this chapter.

2.Principles of Operation

2.1.Motion of a single ion

Charged particles interact strongly with both electric and magnetic fields and one attractive way to trap such particles would be to put them in a region where there is a three-dimensional (3D) minimum of the electrostatic potential, so that there is a force toward the center of the trap from all directions. 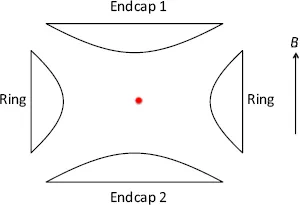However, this is disallowed by Earnshaw’s theorem, which follows from the Poisson equation for the electrostatic potential ϕ in the absence of free charges, ∇²ϕ(x, y, z) = 0. As a result, electrostatic fields can be used to trap along at most two axes, and in order to make a 3D trap, some other mechanism must be used to confine the motion in the remaining direction(s). One way of achieving this is to add a uniform magnetic field

which can effectively confine the motion in the radial (x, y) directions by forcing the particle into circular orbits. If this is combined with a quadratic electrostatic potential,

Fig. 1.Cross-section through the electrodes of a Penning trap. The two endcap electrodes are connected together. A DC potential applied between the endcaps and the ring creates a 3D quadrupole potential in the region between the electrodes. This traps particles along the vertical z-direction. The addition of a uniform magnetic field

along the trap axis ensures 3D trapping. The separation of the endcaps is 2z₀ and the internal diameter of the ring is 2r₀, which is typically of the order of 1 cm (see text).

a stable 3D trap is formed. Here V₀ is the applied trap potential and R² is a parameter related to the size of the trap. The potential described by this equation can be generated by a set of three electrodes having the cross-section shown in Figure 1, in which case R² is equal to

where r₀ and z₀ are the distances from the trap center to the ring and endcap electrodes, respectively. This potential has a saddle point at the center of the trap. Axial trapping is provided by the electric field of the saddle potential, which always provides a restoring force in the axial direction. Radial trapping is achieved with the help of the magnetic field, which provides an inward force for an orbiting particle that is stronger than the outward force in the radial plane arising from the saddle potential.

The equation of motion follows from the Lorentz force,

e(−∇ϕ + v × B), for a particle with mass m and charge e. The axial (z) motion then corresponds to simple harmonic motion (SHM) with an angular oscillation frequency

The equations of motion for the radial (x, y) motion are more complicated due to the presence of the magnetic field, which couples the two equations. However, by defining a complex variable u = x + iy, they can be combined in a single equation,

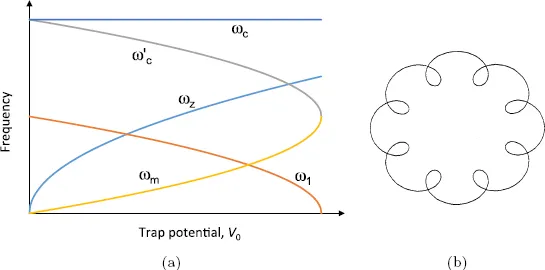
Fig. 2.(a) Plot of the values of the various oscillation frequencies in the Penning trap as a function of the applied trap potential. (b) Typical radial orbit showing a small, fast cyclotron motion superimposed on a larger, slow magnetron orbit.

Here, ω_c = eB/m is the cyclotron frequency. The solution to the radial equation of motion is a superposition of two circular motions, one at the modified cyclotron frequency,

and the other at the magnetron frequency, ω_m = ω_c/2−ω₁. The frequency ω₁ is equal to

and we will see later that it has a simple physical interpretation.

The dependence of the trap oscillation frequencies on the applied trapping potential is shown in Figure 2(a). Note that all three trap oscillation frequencies

are always less than the cyclotron frequency ω_c and that the trap becomes unstable when the trapping potential is such that

At this point, the radial electric field, which pushes the ions away from the trap center, is strong enough to overcome the confining effect due to the magnetic field, so the ions are no longer confined radially. Figure 2(b) shows the path taken by an ion in the radial plane for the particular case that

In many experiments (e.g. high precision mass spectrometry), it is necessary to find the value of the cyclotron frequency accurately. It can be seen that this is given by the sum of the magnetron and modified cyclotron frequencies, i.e.

However, this relation is exact only when the trap is perfect (that is, the potential is described exactly by Equation (1)).

It can be shown in Ref. [10] that the relation,

remains exact even in the presence of misalignments and quadratic imperfections of the field. This equation can therefore be used to obtain accurate values of the cyclotron frequency for real traps that are not perfect.

It is worth noting here that although the axial motion is straightforward SHM, there are anomalies associated with the modified cyclotron and magnetron motions. As a result, the principle of equipartition of energy does not apply to these motions. The anomalies stem from ...

Table of contents

• Cover Page
• Title
• Copyright
• Dedication
• Preface
• Contents
• 1. Penning Traps
• 2. Radiofrequency Traps
• 3. The Guiding Center Approximation
• 4. Toroidal Systems
• 5. Ultrahigh Vacuum for Trapped Ions
• 6. Laser Cooling Techniques Applicable to Trapped Ions
• 7. Non-Laser Cooling Techniques
• 8. Numerical Simulations of Ion Cloud Dynamics
• 9. Plasmas in Penning Traps
• 10. Plasma Modes
• 11. RotatingWall Technique and Centrifugal Separation
• 12. Correlations in Trapped Plasma
• 13. Autoresonance
• 14. Antihydrogen Physics
• 15. Ion Coulomb Crystals and their Applications
• 16. Cold Molecular Ions in Traps
• 17. Precise Tests of Fundamental Symmetries with Trapped Ions
• 18. Trapped-Ion Optical Frequency Standards
• Index