Undergraduate Convexity

Problems and Solutions

Mikkel Slot Nielsen, Victor Ulrich Rohde;;;

• Publisher: WSPC
• Year: 2016
• Topic: Mathematics
• eBook ISBN:
  9789813143661
• Subtopic: Geometry
• Index: Mathematics

-->

This solutions manual thoroughly goes through the exercises found in Undergraduate Convexity: From Fourier and Motzkin to Kuhn and Tucker. Several solutions are accompanied by detailed illustrations and intuitive explanations. This book will pave the way for students to easily grasp the multitude of solution methods and aspects of convex sets and convex functions.

-->

Request Inspection Copy

-->

Chapter 1

Fourier-Motzkin elimination

1.1Introduction

Just like its Gaussian counterpart, Fourier-Motzkin elimination quickly becomes very natural with a bit of practice. The exercises below focus exactly on this practice, and the reader will hopefully feel confident in working with inequalities after carefully going through the material. Some exercises have a more applied flavor and may also serve as a motivation for reducing a system of inequalities.

Being cumbersome, space consuming, and slightly trivial to rewrite the Fourier-Motzkin elimination in detail in every solution, the later solutions become more concise; so, feeling a bit lost may be resolved by simply going back a couple of solutions.

Proposition 1.1. Let α₁, …, α_r, β₁, …β_s ∈ ℝ. Then

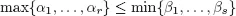
if and only if α_i ≤ β_i for every i, j with 1 ≤ i ≤ r and 1 ≤ j ≤ s:

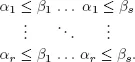
Definition 1.4. The subset

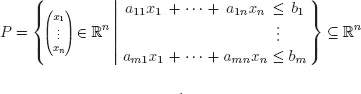
of solutions to a system

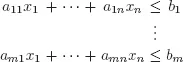
of finitely many linear inequalities (here a_ij and b_i are real numbers) is called a polyhedron.

Whilst Proposition 1.1 is very useful for computation, the following result is more of theoretical interest.

Theorem 1.6.Consider the projection π : ℝⁿ → ℝⁿ⁻¹ given by

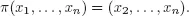
If P ⊆ ℝⁿ is a polyhedron, then

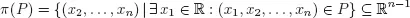
is a polyhedron.

1.2Exercises and solutions

Exercise 1.1. Sketch the set of solutions to the system

of linear inequalities. Carry out the elimination procedure for (1.1) as illustrated in §1.1.

Solution 1.1. The set of solutions is sketched in Figure 1.1. To carry out the elimination procedure we start by isolating x which gives the new system

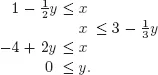
This is, according to Proposition 1.1, equivalent to the system

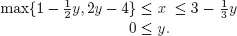
There exists x such that (x, y) is a solution if and only if y satisfies

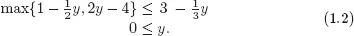
By another use of Proposition 1.1 we know that y is a solution to (1.2) if and only if y is a solution to

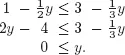
This system is equivalent to

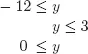
which means that a solution satisfies y ∈ [0, 3]. In conclusion, we have (x, y) ∈ ℝ² is a solution if and only if y ∈ [0, 3] and

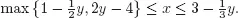
Exercise 1.2. Let

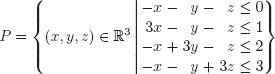
and π : ℝ³ → ℝ² be given by π(x, y, z) = (y, z).

(i)Compute π(P) as a polyhedron i.e., as the solutions to a set of linear inequalities in y and z.

(ii)Compute η(P), where η : ℝ³ → ℝ is given by η(x, y, z) = x.

(iii)How m...

Table of contents

• Cover Page
• Title
• Copyright
• Preface
• Acknowledgements
• Contents
• 1. Fourier-Motzkin elimination
• 2. Affine subspaces
• 3. Convex subsets
• 4. Polyhedra
• 5. Computations with polyhedra
• 6. Closed convex subsets and separating hyperplanes
• 7. Convex functions
• 8. Differentiable functions of several variables
• 9. Convex functions of several variables
• 10. Convex optimization
• Appendix A Analysis
• Appendix B Linear (in)dependence and the rank of a matrix