Models of Bounded Rationality and Mechanism Design

Jacob Glazer, Ariel Rubinstein

• Publisher: WSPC
• Year: 2016
• eBook ISBN: 9789813141346
• Topic: Economics
• Subtopic: Economic Theory
• Index: Economics

This book brings together the authors' joint papers from over a period of more than twenty years. The collection includes seven papers, each of which presents a novel and rigorous model in Economic Theory.All of the models are within the domain of implementation and mechanism design theories. These theories attempt to explain how incentive schemes and organizations can be designed with the goal of inducing agents to behave according to the designer's (principal's) objectives. Most of the literature assumes that agents are fully rational. In contrast, the authors inject into each model an element which conflicts with the standard notion of full rationality, demonstrating how such elements can dramatically change the mechanism design problem.Although all of the models presented in this volume touch on mechanism design issues, it is the formal modeling of bounded rationality that the authors are most interested in. A model of bounded rationality signifies a model that contains a procedural element of reasoning that is not consistent with full rationality. Rather than looking for a canonical model of bounded rationality, the articles introduce a variety of modeling devices that will capture procedural elements not previously considered, and which alter the analysis of the model.The book is a journey into the modeling of bounded rationality. It is a collection of modeling ideas rather than a general alternative theory of implementation.

Chapter 1

An Extensive Game as a Guide for Solving a Normal Game^*

Jacob Glazer

Faculty of Management, Tel Aviv University

Ariel Rubinstein

School of Economics, Tel-Aviv University, and
Department of Economics, Princeton University

We show that for solvable games, the calculation of the strategies which survive iterative elimination of dominated strategies in normal games is equivalent to the calculation of the backward induction outcome of some extensive game. However, whereas the normal game form does not provide information on how to carry out the elimination, the corresponding extensive game does. As a by-product, we conclude that implementation using a subgame perfect equilibrium of an extensive game with perfect information is equivalent to implementation through a solution concept which we call guided iteratively elimination of dominated strategies which requires a uniform order of elimination.

Journal of Economic Literature Classification Numbers: C72.

1.Introduction

Game theory usually interprets a game form as a representation of the physical rules which govern a strategic interaction. However, one can view a game form more abstractly as a description of a systematic relationship between players’ preferences and the outcome of the situation. Consider, for example, a situation which involves two players, 1 and 2. The players can go out to either of two places of entertainment, T or B, bringing with them a third (passive) party L or R. The two players have preferences over the four possible combinations of place and companion. The three presuppositions regarding the situation are:

(i)Player 2’s preferences over the companion component are independent of the place of entertainment.

(ii)Player 2 decides on L or R.

(iii)Player 1 decides on T or B.

Game theory suggests two models to describe this situation. One model would describe the players as playing the game G (see Fig. 1) with the outcome determined by the solution of successive elimination of weakly dominated strategies. The other would say that the players are involved in the game Γ (see Fig. 2) and that the solution concept is one of backward induction. Each alternative summarizes all of the information we possess about the situation. However, the description of the situation via an extensive game is more informative than that via a normal game form since the former provides a guide for easier calculation of the outcome for any given profile of preferences which is consistent with (i).

Figure 1.

Figure 2.

In this paper we elaborate on this idea. We begin in Section 2 by introducing the notion of a “guide” for solving normal form games through iterative elimination of dominated strategies. A guide is a sequence of instructions regarding the order of elimination. In Section 3 we establish that the information about the procedure of solving a normal form game provided by the guide is essentially identical to the additional information provided when the game is described in its extensive form rather than its normal form. As a by-product, we show in Section 4 that implementation by subgame perfect equilibrium (SPE) in an extensive game is equivalent to implementation through a solution concept, which we call guided iteratively undominated strategies, in a normal game which requires a uniform order of elimination.

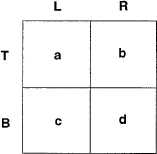
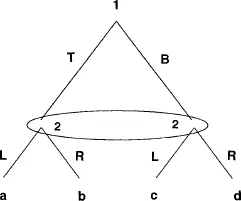
2.Preliminaries

Let N be a set of players and C a set of consequences. A preference profile is a vector of preferences over C, one preference for each player. In order to simplify the paper we confine our analysis to preferences which exclude indifferences between consequences.

(a)Normal Game Form

A normal game form is G = 〈×_i∈N S_i, g〉, where S_i is i’s strategy space and g : ×_i∈N S_i → C is the consequence function. (Without any loss of generality, assume that no strategy in S_i has the name of a subset of S_i.) A game form G accompanied by a preference profile p = {≥_i}_i∈N is a normal game denoted by 〈G, p〉. We say that the strategy s_i ∈ S_i dominates the strategy

for any profile s_−i ∈ ×_j≠iS_j. By this definition one strategy dominates the other even if

for all s_−i.

(b)Guide

A guide for a normal form G is a list of instructions for solving games of the type 〈G, p〉. Each instruction k consists of a name of player i_k and a set A_k. The sublist of instructions for which i_k = i can be thought of as a “multi-round tournament” whose participants are the strategies in S_i. The first instruction in this sublist is a set of at least 2 strategies for player i. One of these strategies will be thought of as a winner (in a sense that will be described later). The losers leave the tournament and the winner receives the name of the subset in which he won. Any element in the sublist is a subset of elements which are left in the tournament. Such an element is either a strategy in S_i which has not participated in any previous round of the tournament, or a strategy which won all previous rounds in which it participated; this strategy appears under the name of the last round in which it won. Following completion of the last round, only one strategy of player i remains a non-loser. Thus, for example, if S₁ = {x₁, x₂, x₃, x₄, x₅}, a possible subl...

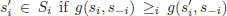
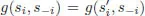
Table of contents

• Cover
• Halftitle
• Series Editors
• Title
• Copyright
• Contents
• Introduction
• 1. An Extensive Game as a Guide for Solving a Normal Game, Journal of Economic Theory, 70 (1996), 32–42.
• 2. Motives and Implementation: On the Design of Mechanisms to Elicit Opinions, Journalof Economic Theory, 79 (1998), 157–173.
• 3. Debates and Decisions, On a Rationale of Argumentation Rules, Games and Economic Behavior, 36 (2001), 158–173.
• 4. On Optimal Rules of Persuasion, Econometrica, 72 (2004), 1715–1736.
• 5. A Study in the Pragmatics of Persuasion: A Game Theoretical Approach, Theoretical Economics, 1 (2006), 395–410.
• 6. A Model of Persuasion with Boundedly Rational Agents, Journal of Political Economy, 120 (2012), 1057–1082.
• 7. Complex Questionnaires, Econometrica, 82 (2014), 1529–1541.