Introduction to General Relativity and Cosmology

Christian G Böhmer

• Publisher: WSPC (EUROPE)
• Year: 2016
• eBook ISBN: 9781786341204
• Topic: Physical Sciences
• Subtopic: Geometry

-->

Introduction to General Relativity and Cosmology gives undergraduate students an overview of the fundamental ideas behind the geometric theory of gravitation and spacetime. Through pointers on how to modify and generalise Einstein's theory to enhance understanding, it provides a link between standard textbook content and current research in the field.

Chapters present complicated material practically and concisely, initially dealing with the mathematical foundations of the theory of relativity, in particular differential geometry. This is followed by a discussion of the Einstein field equations and their various properties. Also given is analysis of the important Schwarzschild solutions, followed by application of general relativity to cosmology. Questions with fully worked answers are provided at the end of each chapter to aid comprehension and guide learning. This pared down textbook is specifically designed for new students looking for a workable, simple presentation of some of the key theories in modern physics and mathematics.

-->

Request Inspection Copy

-->

1

Differential Geometry

The theory of General Relativity is a theory of gravitation based on the geometric properties of spacetime. Its formulation requires the use of differential geometry. One of the great difficulties when working with geometric objects on arbitrary spaces is notation. As far as Cartesian tensors are concerned, the issue is much easier. However, in order to prepare for the later parts on Riemannian and Lorentzian geometry, we will introduce most of the abstract notation of differential geometry in the familiar Euclidean setting.

1.1. The Concept of a Vector

Let us start with Euclidean space denoted by

. A vector v is a quantity in

with specified direction and magnitude. The magnitude of this vector is denoted either by |υ| or υ. Graphically we can view a vector as an arrow, with its length representing the magnitude. Various physical quantities are best represented by vectors, examples are forces, velocities, moments, displacements and many others. We define the zero vector O as a vector with zero magnitude and arbitrary direction. For any vector υ, we can define a unit vector pointing in the same direction as υ but with magnitude 1, simply by

Two vectors are called equal if they have the same direction and the same magnitude.

The concept of a vector as such does not require the introduction of coordinates. This is important conceptually, the outcome of an experiment should not depend on our choice or coordinates. In most applications, however, a choice of good coordinates which are adapted to the physical system can considerably simplify subsequent equations. Try for instance solving the two simple equations ẍ = 0, ӱ = 0 using polar coordinates, it becomes difficult.

However, choosing coordinates and units can also lead to substantial problems. In particular, when two groups working on the same project assume they use the same coordinates. It was exactly this assumption that made NASA’s Mars Climate Orbiter mission a failure. Subcontractor Lockheed Martin designed thruster software that used Imperial units, while NASA uses metric units in their software. The spacecraft approached Mars at a much lower altitude than expected and it is likely that atmospheric stresses destroyed it (NASA, 1999). As trivial as the matter seems to appear, units, coordinates and their transformation properties are a crucial ingredient of Engineering, Mathematics and Physics. It also explains why theoretical physicists are keen to set every possible constant to one.

1.1.1. Vector operations

Having introduced the concept of a vector, we must next define admissible algebraic operations on vectors. Let u and υ be two vectors, then we define their sum u + υ to be the vector which completes the triangle when the tail of υ is placed at the tip of u. When u and υ are interchanged, one arrives at the same vector (parallelogram rule) and thus u + υ = υ + u. We can also multiply the vector υ by an arbitrary real number r ∈ ℝ to get the vector rυ. This vector has the same direction as υ if r > 0 but has opposite direction if r < 0 and it has length |r||υ|. When r = 0, we get the zero vector. Addition and the notion of the zero vector allow us to define the inverse (under addition) of a vector by saying that

is the inverse of υ if

We will denote this simply by

We can now state what is meant by the operation u − υ, namely this vector obtained by placing the tip of υ at the tip of u.

Two vectors uniquely define a plane. Let us move the ...

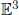
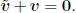
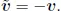
Table of contents

• Cover Page
• Title
• Copyright
• Dedication
• Preface
• About the Author
• Contents
• 1. Differential Geometry
• 2. Einstein Field Equations
• 3. Schwarzschild Solutions
• 4. Cosmology
• 5. Solutions to Exercises
• Bibliography
• Index