Geometry In Advanced Pure Mathematics

0

Shaun Bullett, Tom Fearn;Frank Smith;;

• Publisher: WSPC (EUROPE)
• Year: 2017
• ISBN:
  9781786341099
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

-->

This book leads readers from a basic foundation to an advanced level understanding of geometry in advanced pure mathematics. Chapter by chapter, readers will be led from a foundation level understanding to advanced level understanding. This is the perfect text for graduate or PhD mathematical-science students looking for support in algebraic geometry, geometric group theory, modular group, holomorphic dynamics and hyperbolic geometry, syzygies and minimal resolutions, and minimal surfaces.

Geometry in Advanced Pure Mathematics is the fourth volume of the LTCC Advanced Mathematics Series. This series is the first to provide advanced introductions to mathematical science topics to advanced students of mathematics. Edited by the three joint heads of the London Taught Course Centre for PhD Students in the Mathematical Sciences (LTCC), each book supports readers in broadening their mathematical knowledge outside of their immediate research disciplines while also covering specialized key areas.

-->

Chapter 1

Algebraic Geometry

Ivan Tomašić

School of Mathematical Sciences

Queen Mary University of London

London E1 4NS, UK

[email protected]

Some of the most beautiful chapters of pure mathematics of the 20th century were motivated by considerations around Weil conjectures for zeta functions of algebraic varieties over finite fields. The purpose of these notes is to introduce the reader to enough algebraic geometry to be able to understand some elementary aspects of their proof for the case of algebraic curves and appreciate their number-theoretic consequences.

1.Introduction

Intuitively speaking, algebraic geometry is the study of geometric shapes that can be locally (piecewise) described by polynomial equations.

The main advantage of restricting our attention to polynomial expressions is their versatility, given that they make sense in completely arbitrary rings and fields, including the ones which carry no intrinsic topology. This gives a ‘universal’ geometric intuition in areas where classical geometry and topology fail.

Consequently, methods of algebraic geometry apply in a range of mathematical disciplines, depending on the choice of rings or fields in which to solve our polynomial systems. In geometry we typically work over R or C, while in number theory we choose arithmetically significant structures, such as Z or Q (in Diophantine geometry), number fields, p-adic numbers, or even structures of positive characteristic and finite fields.

We focus on the problem of counting points on varieties over finite fields and the associated Weil conjectures in Section 4. We prove the rationality conjecture in an elementary way, as well as using étale cohomology as a ‘black-box’, and we outline the approach to the functional equation.

1.1.Solving polynomial equations

Let f(x, y) be a polynomial over a ring k, and let X be the ‘plane curve’ defined by the equation f(x, y) = 0. For any ring R extending k, we can consider the solution set

Example 1.1 (Diophantine geometry). Let X be a regular/smooth projective curve of genus g (Definitions 3.7 and 3.39) defined over k = Q. Intuitively, g is the number of ‘holes’ in X(C) conside...

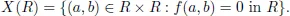
Table of contents

• Cover
• Halftitle
• Series Editors
• Title
• Copyright
• Preface
• Contents
• Chapter 1. Algebraic Geometry
• Chapter 2. Introduction to the Modular Group and Modular Forms
• Chapter 3. Geometric Group Theory
• Chapter 4. Holomorphic Dynamics and Hyperbolic Geometry
• Chapter 5. Minimal Surfaces and the Bernstein Theorem
• Chapter 6. Syzygies and Minimal Resolutions