Computational Physics

An Introduction to Monte Carlo Simulations of Matrix Field Theory

Badis Ydri

• Publisher: WSPC
• Year: 2017
• ISBN:
  9789813200234
• Topic: Physical Sciences
• Subtopic: Nuclear Physics

This book is divided into two parts. In the first part we give an elementary introduction to computational physics consisting of 21 simulations which originated from a formal course of lectures and laboratory simulations delivered since 2010 to physics students at Annaba University. The second part is much more advanced and deals with the problem of how to set up working Monte Carlo simulations of matrix field theories which involve finite dimensional matrix regularizations of noncommutative and fuzzy field theories, fuzzy spaces and matrix geometry. The study of matrix field theory in its own right has also become very important to the proper understanding of all noncommutative, fuzzy and matrix phenomena. The second part, which consists of 9 simulations, was delivered informally to doctoral students who were working on various problems in matrix field theory. Sample codes as well as sample key solutions are also provided for convenience and completeness.

PART 2

Monte Carlo Simulations of Matrix Field Theory

Chapter 10

Metropolis Algorithm for Yang–Mills Matrix Models

10.1Dimensional Reduction

10.1.1Yang–Mills Action

In a four dimensional Minkowski spacetime with metric g_µν = (+1, −1, −1, −1), the Yang–Mills action with a topological theta term is given by

We recall the definitions

The path integral of interest is

This is invariant under the finite gauge transformations A_µ

g⁻¹ A_µg + ig⁻¹ ∂_µg with g = e^iΛ in some group G (we will consider mostly SU(N)).

We Wick rotate to Euclidean signature as x⁰

x⁴ = ix⁰ and as a consequence d⁴x

d⁴_Ex = id⁴x, ∂₀

∂₄ = −i∂₀ and A₀

A₄ = −iA₀. We compute F_µν F^µν

(F²_µν)_E and

We get then

We remark that the theta term is imaginary. In the following we will drop the subscript E for simplicity. Let us consider first the θ = 0 (trivial) sector. The pure Yang–Mills action is defined by

The path integral is of the form

First we find the equations of motion. We have

The equations of motion for variations of the gauge field which vanish at infinity are therefore given by

Equivalently

We can reduce to zero dimension by assuming that the configurations A_a are constant configurations, i.e. are x-independent. We employ the notation A_a = X_a. We obtain immediately the action and the equations of motion

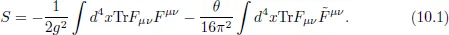
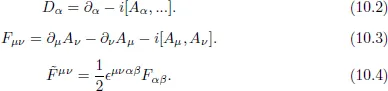
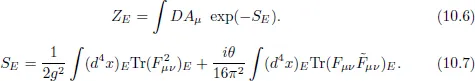
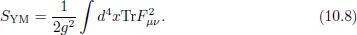
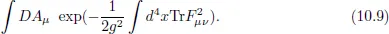
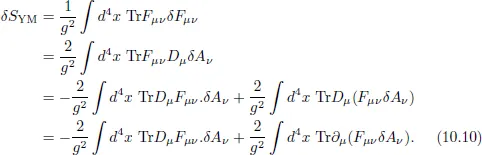
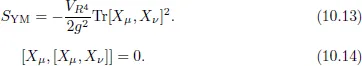
10.1.2Chern–Simons Action: Myers Term

Next we consider the general sector θ ≠ 0. First we show that the second term in the action S_E does not affect the equations of motion. In other words, the theta term is only a surface term. We define

We compute the variation

We use the Jacobi identity

Thus

This shows explicitly that the theta term will not contribute to the equations of motion for variations of the gauge field which vanish at infinity.

In order to find the current K_α itself we adopt the method of [1]. We consider a one-parameter family of gauge fields A_µ(x, τ) = τ A_µ(x) with 0 ≤ τ ≤ 1. By using the above result we have immediately

By integrating both sides with respect to τ between τ = 0 and τ = 1 and setting K_α(x, 1) = K_α(x) and K_α(x, 0) = 0 we get

The theta term is proportional to an integer k (known variously as the Pontryagin class, the winding number, the instanton number and the topological charge) defined by

Now we imagine that the four-dimensional Euc...

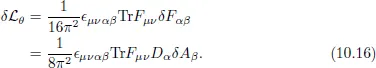
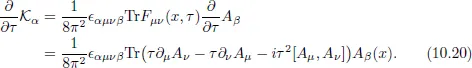
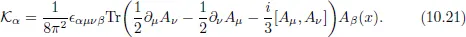
Table of contents

• Cover
• Halftitle
• Title
• Copyright
• Dedication
• Preface
• Contents
• Introductory Remarks
• Introduction to Computational Physics
• Monte Carlo Simulations of Matrix Field Theory
• Index