Let Us Use White Noise

0

T Hida, L Streit;;;

• Publisher: WSPC
• Year: 2017
• eBook ISBN: 9789813220959
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

-->

Why should we use white noise analysis? Well, one reason of course is that it fills that earlier gap in the tool kit. As Hida would put it, white noise provides us with a useful set of independent coordinates, parametrized by "time". And there is a feature which makes white noise analysis extremely user-friendly. Typically the physicist — and not only he — sits there with some heuristic ansatz, like e.g. the famous Feynman "integral", wondering whether and how this might make sense mathematically. In many cases the characterization theorem of white noise analysis provides the user with a sweet and easy answer. Feynman's "integral" can now be understood, the "It's all in the vacuum" ansatz of Haag and Coester is now making sense via Dirichlet forms, and so on in many fields of application. There is mathematical finance, there have been applications in biology, and engineering, many more than we could collect in the present volume.

Finally, there is one extra benefit: when we internalize the structures of Gaussian white noise analysis we will be ready to meet another close relative. We will enjoy the important similarities and differences which we encounter in the Poisson case, championed in particular by Y Kondratiev and his group. Let us look forward to a companion volume on the uses of Poisson white noise.

The present volume is more than a collection of autonomous contributions. The introductory chapter on white noise analysis was made available to the other authors early on for reference and to facilitate conceptual and notational coherence in their work.

-->

Chapter 1

White Noise Analysis: An Introduction

Maria João Oliveira

Universidade Aberta, P 1269-001 Lisbon, Portugal
CMAF-CIO, University of Lisbon, P 1749-016 Lisbon, Portugal
[email protected]

The starting point of White Noise Analysis¹¹ and^{2,14–16,20,21,34,39} is a real separable Hilbert space H with inner product (·, ·) and the corresponding norm | · |, and a nuclear triple

where N is a nuclear space densely and continuously embedded in H. Of course, in a general framework, a priori there are several different possible nuclear spaces. However, in concrete applications, the application will suggest the use of particular nuclear triples. For example, in the study of intersection local times of d-dimensional Brownian motions it is natural to consider the space H = L²(R, R^d) =: L²_d(R) of all vector valued square integrable functions with respect to the Lebesgue measure on R and the Schwartz space N = S(R, R^d) =: S_d(R) of vector valued test functions, while in the treatment of Feynman integrals the spaces L²(R) := L²(R, R), S(R) := S(R, R) are the natural ones.

Since nuclear triples are the basis of the whole White Noise Analysis, we start by briefly recalling the main background of the theory of nuclear spaces, due to A. Grothendieck.⁷ For simplicity, instead of general nuclear spaces, cf. e.g.,^40,42,45,50 we just consider nuclear Fréchet spaces, which are the only ones needed in this book. For more details and the proofs see e.g.^2,3,9,14.

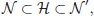
1.Nuclear Triples

As before, let H be a real separable Hilbert space. We consider a family of real separable Hilbert spaces H_p, p ∈ N, with Hilbertian norm | · |_p such that

so that the corresponding system of norms is ordered:

In addition, we assume that the intersection of the Hilbert spaces H_p, denoted by

is dense in each space H_p, p ∈ N.

Definition 1. The linear space N is called nuclear whenever for every p ∈ N there is a q > p such that the canonical embedding H_q

H_p is a Hilbert-Schmidt operator.

From now on we shall assume that all spaces (1) are nuclear and fix on N the projective limit topology, that is, the coarsest topology on N with...

Table of contents

• Cover
• Halftitle
• Title
• Copyright
• Preface
• Contents
• 1. White Noise Analysis: An Introduction
• 2. Quantum Fields
• 3. Feynman Path Integrals
• 4. Local Times in White Noise Analysis
• 5. White Noise Analysis and the Chern-Simons Path Integral
• 6. A White Noise Approach to Insider Trading
• 7. Outlook of White Noise Theory
• Subject Index