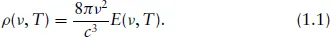Quantum Mechanics

Its Early Development and the Road to Entanglement and Beyond

Edward G Steward

• Publisher: ICP
• Year: 2011
• eBook ISBN: 9781911298649
• Topic: Physical Sciences
• Subtopic: Mathematical & Computational Physics

This book provides the reader with an explanation of the origin and establishment of quantum mechanics together with a descriptive survey of developments up to the present day. The mathematics is presented in a digestible form yet following the original approach.

This second edition presents two new chapters to supplement and extend the first edition material. “Interpretations of Quantum Mechanics” surveys a wide range of current topics, including the multiverse, 't Hooft's ideas for a deterministic local field theory, a summary of the de Broglie-Bohm pilot-wave theory and Anthony Valentini's development of it, and speculative concluding comments on the way ahead.

“A Reflective Interlude” looks in more detail than hitherto at the origin and early years of wave-particle duality, with emphasis on trying to discover, as far as possible, what was the physical reality implied by de Broglie's work as it progressed.

Appendices include useful reminder notes on associated background topics, with a new appendix “Planck Units”.

With references to the original works, to reviews and useful bibliographies, the reader is uniquely well-equipped to delve further into the subject.

In addition to its importance for those studying physics, this book is also intended for those studying the history of science.

Chapter 1

Setting the Scene

1.1.Introduction

Quantum Mechanics is commonly defined as the system of mechanics that was developed from Quantum Theory to explain the properties of atoms and molecules. Quantum Theory itself had earlier been established as a consequence of Planck’s introduction in 1900 of the concept of ‘energy elements’ (named ‘energy quanta’ by Einstein in 1905(a)) to resolve the inability of Classical Physics to account fully for the spectrum of radiation from a hot body (‘black-body radiation’ explained below). However, the concept of ‘energy elements’ could equally well have been arrived at, and probably more easily, in resolving other problems confronting Classical Physics at the end of the 19th century — for example the failure to explain the specific heat of solids at low temperatures, or why in the photoelectric effect the energy of ejected photoelectrons depends only on the frequency of the incident light and not its intensity.

A number of developments led to the establishment of a ‘quantum mechanics’. Firstly, Planck’s discovery immediately overturned the universally accepted notion in Classical Physics that energy is a continuous variable. Instead, it is ‘granular’ and ‘discrete’, to quote descriptions often used. That concept was taken forward crucially in 1905 by Einstein, who explained details in the photoelectric effect by proposing that radiation itself is ‘quantised’, a concept alien to Planck who only saw its generation as involving elemental energy units.

Then, in 1913, Bohr showed the role of the quantum concept in explaining the stability of Rutherford’s 1911 planetary model of the atom, in terms of ‘stationary states’. In 1923 came de Broglie’s suggestion that the concept of wave–particle duality of light, resulting from Einstein’s quantum explanation of the photoelectric effect, also applies to matter particles. In the hands of Schrödinger, Heisenberg, Born, Dirac and others, ‘quantum mechanics’ was born. These form the subject of Chaps. 7 and 8.

It is fascinating to realise that the basic discoveries by Planck, Einstein and Bohr sprang from earlier studies of the radiation from the Sun and the colour of flames. It was largely the work on those topics by Kirchhoff in 1859–1860 that provided the fertile ground. Sections 1.2 and 1.3 briefly outline how that came about. (Kirchhoff was already known for his laws in 1845 concerning electrical networks — work foreshadowing Maxwell’s 1864 Electromagnetic Theory of radiation.)

In §1.4, we set the scene for Planck’s work on tackling the problem mentioned above concerning the explanation of the details of the observed spectrum of heat radiation — the subject of Chap. 3. Then, in §1.5 we note the problems concerning the nature of light, and indicate how this led to Einstein’s Special Theory of Relativity. This is the subject of Chap. 2, and it played a major role in the development of the Quantum Theory and Quantum Mechanics. Finally, in §1.6, we briefly note the range of outstanding contributions made by Einstein, referred to in various parts of this book, and the arrival of the concepts of Complementarity, the Uncertainty Principle, the Copenhagen Interpretation, and ‘entanglement’, that are the subjects of Chaps. 9 and 10.

1.2.Light and Heat: Kirchhoff’s ‘Black-body Radiation’

Key steps leading to the way in which Kirchhoff’s work revealed the problem that Planck was to solve can be summarised as follows:

1800	Herschel showed that heat radiation (e.g. the heat of sun-light) is the extension into the infrared, i.e. beyond the red end of the visible light spectrum. He did this by using a prism and moving a thermometer along the spectrum produced by sunlight.
1802	Wollaston showed that the solar spectrum contains ‘dark’ lines.
1822	Fraunhofer had by now measured the dark lines using a diffraction grating. He found that the strongest (a doublet) was at the same position as the yellow light of many flames.
1826	Fox Talbot studied the colours of flames containing different substances, showing the potential for the use of spectroscopy in chemical analysis.
1833	W. H. Miller suggested that the Fraunhofer dark lines in the solar spectrum were due to absorption in the outer layers of the Sun.
1833	Ritchie demonstrated experimentally, in an elegantly simple way (described in elementary textbooks), the proportionality of the heat-emitting and heat-absorbing powers of a surface.
1858	Balfour Stewart showed that a radiating body in equilibrium at a given temperature emits and absorbs radiation at equal rates (Prévost’s 1791 Theory of Exchanges) applies at all wavelengths, i.e. to light as well as heat radiation.
1859	Kirchhoff, independently of Balfour Stewart, and more rigorously, came to the same conclusion. In Kirchhoff’s classic paper presented in 1859, entitled ‘On the relation between the emission and absorption of light and heat’, he used thermodynamic principles to show that “for rays of the same wavelength the ratio of the emissive power to the absorptivity, at the same temperature, is the same for all bodies”. This was subsequently known as ‘Kirchhoff’s Law’, and more rigorous proofs followed.
	It was in a second paper that Kirchhoff introduced the notion of what he called a ‘black-body’, defining it as a body that absorbs all the radiation incident upon it. Together with the theorem, it meant that with such a ‘black-body’ one could have an equilibrium spectral distribution independent of everything except the temperature. This was clearly of enormous fundamental significance.
	A close approximation to a black-body was achieved by constructing a cavity with highly-insulating walls and closed except for a very small orifice. Experimental studies of the radiation were made and it became increasingly evident that the details could not be explained by classical methods. That is where evidence of the quantum nature of energy became apparent, and that is the subject of Chap. 3.

1.3.Kirchhoff’s Work on Optical Spectra

Not only had Kirchhoff’s concept of black-body radiation led to Planck’s discovery of the ‘energy quantum’, but in his work leading to the formulation of his theorem he had explored in more detail Fraunhofer’s observations that the dark lines in the solar spectrum coincided with the bright lines in the spectra of flames. He, and others, were able to show that chemical elements have unique, characteristic spectra, and that the emission and absorption frequencies are the same for a given element — this became known as Kirchhoff’s ‘law of radiation’. The solar dark line (a doublet) was identified with the D-line doublet of sodium.

This aspect of Kirchhoff’s work led to the other major discovery of the role of the quantum concept. It came about as follows.

With Bunsen, Kirchhoff studied the solar spectrum in more detail and by 1860 he was able to identify the chemical elements in the atmosphere of the Sun. This was the foundation of chemical spectroscopy and it also led to a new era in astronomy. However, problems lay ahead.

As an extension of Kirchhoff’s work, Balmer produced in 1885 an empirical formula for the hydrogen spectrum, but a scientific basis was lacking. In 1911, Rutherford’s planetary model of the atom was deduced from experiments by Geiger and Marsden, at the suggestion of Rutherford, on the scattering of α-particles by a thin gold foil. However, the stability of such an orbital system, in which orbital electrons would, classically, be expected to spiral into the nucleus, was unexplained. In 1913, Bohr showed that if one introduced the concept of orbital ‘stationary states’ between which discrete, quantised, transitions occur, then the observed spectral lines could be explained. But what was the nature of the ‘stationary states’? The way in which that was resolved is the subject of Chap. 5, with further developments in Chap. 7.

1.4.Planck’s Route to Tackling the Black-body Radiation Problem

Planck’s approach to dealing with the black-body radiation problem was by a circuitous route.

In his formative years as a physicist he was influenced very much by the writings of Clausius, especially with regard to the Second Law of Thermodynamics. Based on experimental observations, the Second Law was variously expressed, but to the effect that it is impossible to cause heat to pass from one body to another at a higher temperature without the expenditure of mechanical work. Then, in 1865, Clausius introduced the concept of entropy and reformulated the Second Law to state that the entropy of an isolated system always increases or remains constant (see Appendix A), i.e. changes are irreversible.

Strongly believing in the absolute validity of the Second Law, Planck was opposed to the statistics approach that Boltzmann took to thermal equilibrium, in which Boltzmann was following Maxwell’s earlier view of the Second Law as statistical in nature, and which did not exclude the possibility of reversibility. Planck’s opposition to the idea of reversibility and his preference for Classical Thermodynamics was going to influence him when his attention turned to the black-body radiation problem. However, as we shall see in Chap. 3, he found that he had to change reluctantly to a ‘probabilistic’ approach, though not using Boltzmann statistics.

Another topic on which Planck had worked prior to tackling the black-body problem, and which was also going to influence him, was triggered by his learning of Hertz’s discovery in 1887 of the electromagnetic waves emitted by oscillating charges (seen as an important confirmation of Maxwell’s electromagnetic theory). It led Planck to visualise black-body radiation as originating in sub-microscopic linear harmonic oscillators, or ‘resonators’ (the simplest body that can absorb and emit radiation) in the walls of a black-body cavity as conceived by Kirchhoff (which involved no stipulation about the nature of the cavity wall). It led him to derive the following expression relating the black-body radiation frequency distribution, ρ (ν, T), to the average equilibrium energy, E (ν, T), of a (damped) harmonic oscillator of frequency ν at temperature T in a cavity wall:

This ‘theorem’ was to form the basis of much that followed and it played an important role in Einstein’s subsequent studies.

To determine ρ(ν, T), it was of course necessary to determine E(ν, T) and that is where the difficulties arose. Suffice it to say here that using the Equipartition of Energy Principle of Classical Physics led to a distribution that was not in accord with experimental data.

With the resonators that Planck envisaged, quite legitimately as we have noted, as a model for the emitters/absorbers in the walls of a black-body cavity, and his strong belief in the Second Law of thermodynamics, he embarked on tackling the problem that was arising in finding a scientific basis for the experimental measurements of black-body radiation. That is the fascinating story presented in Chap. 3, leading to the birth of the quantum. Before that, we need to recall some relevant aspects concerning the state of knowledge, at that time, about electromagnetic radiation itself.

1.5.Light and the Aether

The transverse wave model of light was established by Young’s double-aperture experiment of 1801, and elaborated by the work of Fresnel around 1815.

Maxwell’s 1864 electromagnetic theory then suggested that the wavemotion of light consists of oscillating electric and magnetic fields travelling through an ‘aether’...

Table of contents

• Cover
• Halftitle
• Title
• Copyright
• Dedication
• Contents
• Acknowledgements
• Preface to the First Edition
• Preface to the Second Edition
• About the Author
• 1. Setting the Scene
• 2. Light: The ‘Aether’ and the Special Theory of Relativity
• 3. Thermal Radiation and Planck’s ‘Energy Elements’
• 4. Einstein and the Quantum
• 5. The Quantum in the Atom: Optical Spectra
• 6. Einstein’s Transition Probabilities: Bohr’s Theory and Planck’s Law
• 7. Wave Mechanics
• 8. Matrix Mechanics
• 9. Complementarity, the Uncertainty Principle, and the Copenhagen Interpretation
• 10. Indeterminacy and Entanglement (Sara M. McMurry)
• 11. A Reflective Interlude
• 12. Interpretations of Quantum Mechanics (Sara M. McMurry)
• Appendices
• Bibliography
• References
• Index