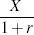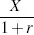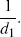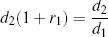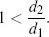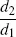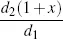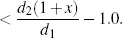Lecture Notes in Fixed Income Fundamentals

Eliezer Z Prisman

• Publisher: WSPC
• Year: 2017
• ISBN:
  9789813149786
• Topic: Economics
• Subtopic: Banks & Banking
• Index: Economics

-->

Written for undergraduates, this book is dedicated to fixed income fundamentals that do not require modeling the dynamics of interest rates. The book concentrates on understanding and explaining the pillars of fixed income markets, using the modern finance approach implied by the "no free lunch" condition. It focuses on conceptual understanding so that novice readers will be familiar with tools needed to analyze bond markets. Institutional information is covered only to the extent that is necessary to obtain full appreciation of concepts.

This volume will equip readers with a solid and intuitive understanding of the No Arbitrage Condition — its link to the existence and estimation of the term structure of interest rates, and to valuation of financial contracts. Using the modern approach of arbitrage arguments, the book addresses positions and contracts that do not require modeling evolution of interest rates. As such, it welcomes readers lacking the technical background for this modeling, and provides them with good intuition for interest rates, no arbitrage condition, bond markets and certain financial contracts.

-->

Chapter 1

Introduction and Review of Simple Concepts

One of the most basic concepts of finance is “time value of money”. Dollars, like quantities in physics, also have a measure of units other than the magnitude measure. This unit measure is the time at which the magnitude of money is available to you to be used. Financial markets offer investors the opportunity to invest their money rather than “keeping it idle”. If you have a certain amount of money, for example $1000, that you do not need now but only in a year, this money can be invested for a year. In most of this book we are concerned with risk-less investments, which means that there are no uncertainties about the return of the investment. It is fixed at the time the investment is made, and the likelihood that it will not be realized as promised is zero. While we shall touch on the meaning of “risk-free” investment in the next section, for now let us just take it for granted. The existence of such risk-free investment possibilities introduces the second dimension (unit) of monies, which is time. Assume that one can get r for each dollar invested for a year. If r for example is 10%, then $1000 today will grow to be 1000(1.10) or in general to 1000 + 1000r. Therefore $1000 today is not equivalent to $1000 a year from today. If one needs $1000 in a year, one only needs to have 1000(1 + r)⁻¹. Given 1000(1 + r)⁻¹ today and investing it for a year generates [1000(1 + r)⁻¹](1 + r) = 1000 which is the required amount. We see therefore that $X in a year is equivalent to

today.

is termed the present value of X. Similarly Y dollars today is equivalent to Y (1 + r) in a year and the latter is termed the future value of Y. The conversion of dollars of a year from now to dollars of today is done by multiplying by (1 + r)⁻¹, which is termed a discount factor. It is usually denoted by d with a sub index of the time. It is a discount factor for a year from now and will be denoted by d₁. The future value of a dollar in a year can thus be written also as

A feature of financial markets therefore is the “opportunity cost” of monies and this is why if one borrows money, one pays for using other peoples’ money. Money can be invested and it increases its value. Hence borrowing $1000 for a year will require returning 1000 + 1000r. In this introduction we assume a very simplistic model whereby borrowing and lending money is done at the same rate and everybody can borrow and lend at the same risk-free rate. Of course the return on the investment depends on the duration of the investment. Obviously a dollar invested for a year will yield less than a dollar invested for two years. Similarly, borrowing for a year will require less interest payments than borrowing for two years. We again start with a simplistic assumption, which will be relaxed very soon, that the interest charge is r per year regardless of the duration the money is either borrowed or invested. This means that if a dollar is invested for a year it will grow to 1 + r₁, and we use r₁ for the interest rate received over a year. If a dollar is invested for 2 years it will grow to 1 + r₂ and the relation between r₁ and r₂ is such that 1 + r₂ =(1 + r₁)(1 + r₁). The interest rate r₂ is also referred to as the simple interest earned over a period of 2 years. The expression (1 + r₁) · (1 + r₁) is referred to as compound interest. It can be interpreted as if the dollar was invested first for a year to grow to (1 + r₁), and then this amount is invested again for a year, at the same rate, to grow to (1 + r₁) · (1 + r₁). Thus at the end of the second year interest is paid also on the interest earned over the first year, and hence the term compound. It is not necessarily the case in the market place that the simple interest rate paid over k years, r_k, satisfies (1 + r₁)^k = 1 + r_k. However, r₂ must be bigger than r₁. If this is the not case, i.e., if r₁ > r₂ then it implies that d₂ =(1 + r₂)⁻¹ will be bigger than d₁ =(1 + r₁)⁻¹. One can thus borrow $ d₂ to be returned in 2 years which means that $1 should be paid in 2 years. Obtaining the $ d₂ one would then invest it for a year to receive

which is more than a dollar. Thus one reaches the end of year one with an amount

At the beginning of the second year, the interest rate that will prevail in the market at the end of year one, for an investment of one year, is not known. However, it will be a positive number say, 0 < x. Thus, investing the at the end of year

one for one year will generate

which is for sure greater than 1. Paying back the loan one would pocket

Clearly, such situations cannot exist in real markets. Such an investment strategy that produces profit with no risk and no out-of-pocket money is called arbitrage. We shall see it in more detail and adapted to more realistic situations in the following chapters. If such a situation exists, investors, being rational, will go for it and as a result will produce demand and supply for money invested and borrowed for different periods. In the above example all investors would demand to borrow money to be returned in 2 years. Since interest rates can...