Lectures on Lie Groups

Wu-Yi Hsiang

• Publisher: WSPC
• Year: 2017
• eBook ISBN: 9789814740739
• Edition: 2
• Topic: Mathematics
• Subtopic: Abstract Algebra
• Index: Mathematics

-->

This volume consists of nine lectures on selected topics of Lie group theory. We provide the readers a concise introduction as well as a comprehensive "tour of revisiting" the remarkable achievements of S Lie, W Killing, É Cartan and H Weyl on structural and classification theory of semi-simple Lie groups, Lie algebras and their representations; and also the wonderful duet of Cartan's theory on Lie groups and symmetric spaces.

With the benefit of retrospective hindsight, mainly inspired by the outstanding contribution of H Weyl in the special case of compact connected Lie groups, we develop the above theory via a route quite different from the original methods engaged by most other books.

We begin our revisiting with the compact theory which is much simpler than that of the general semi-simple Lie theory; mainly due to the well fittings between the Frobenius–Schur character theory and the maximal tori theorem of É Cartan together with Weyl's reduction (cf. Lectures 1–4). It is a wonderful reality of the Lie theory that the clear-cut orbital geometry of the adjoint action of compact Lie groups on themselves (i.e. the geometry of conjugacy classes) is not only the key to understand the compact theory, but it actually already constitutes the central core of the entire semi-simple theory, as well as that of the symmetric spaces (cf. Lectures 5–9). This is the main reason that makes the succeeding generalizations to the semi-simple Lie theory, and then further to the Cartan theory on Lie groups and symmetric spaces, conceptually quite natural, and technically rather straightforward.

--> -->
Contents:

• Linear Groups and Linear Representations
• Lie Groups and Lie Algebras
• Orbital Geometry of the Adjoint Action
• Coxeter Groups, Weyl Reduction and Weyl Formulas
• Structural Theory of Compact Lie Algebras
• Classification Theory of Compact Lie Algebras and Compact Connected Lie Groups
• Basic Structural Theory of Lie Algebras
• Classification Theory of Complex Semi-Simple Lie Algebras
• Lie Groups and Symmetric Spaces, the Classification of Real Semi-Simple Lie Algebras and Symmetric Spaces

--> -->
Readership: Advanced undergraduate and graduate students, and researchers in group theory.
-->Lie Groups;Lie Algebras;Symmetric Groups Key Features:

• Starting with a thorough treatment of the compact theory makes the Lie theory much easier to understand and then, to apply
• Highlights the orbital geometry of conjugacy classes that provides a clean-cut geometric grasp of the entirety of the non-commutativity of Lie group structures — the most crucial core of Lie group structures
• A step-by-step and hand-in-hand geometric as well as algebraic development of the compact theory will make it conceptually more natural and technically much easier for readers to commence such a "tour of revisiting" by themselves

Lecture 1

Linear Groups and Linear Representations

1.Basic Concepts and Definitions

Definitions 1. A topological (resp. Lie) group consists of a group structure and a topological (resp. differentiable) structure such that the multiplication map and the inversion map are continuous (resp. differentiable).

2. A topological (resp. Lie) transformation group consists of a topological (resp. Lie) group G, a topological (resp. differentiable) space X and a continuous (resp. differentiable) action map Φ: G × X → X satisfying Φ(1, x) = x, Φ(g₁, Φ(g₂, x)) = Φ(g₁g₂, x).

3. If the above space X is a real (resp. complex) vector space and, if for all g ∈ G, the maps Φ(g) : X → X : x ↦ Φ(g, x) are linear maps, then G is called a real (resp. complex) linear transformation group.

Notation and Terminology 1. A space X with a topological (resp. differentiable, linear) transformation of a given group G shall be called a topological (resp. differentiable, linear) G-space. In case there is no danger of ambiguity, we shall always use the simplified notation, g · x, to denote Φ(g, x). In such a multiplicative notation, the defining conditions of the action map Φ become the familiar forms of 1 · x = x and g₁ · (g₂ · x) = (g₁g₂) · x.

2. A map f : X → Y between two G-spaces is called a G-map if for all g ∈ G and all x ∈ X, f (g · x) = g · f (x).

3. A linear transformation group Φ : G × V → V, or equivalently, a homomorphism ϕ : G → GL(V), is also called a linear representation of G on V. Two linear representations of G on V₁ and V₂ are said to be equivalent if V₁ and V₂ are G-isomorphic, namely, there exists a linear isomorphism A: V₁ → V₂ such that for all g ∈ G and all x ∈ V₁, A · Φ₁(g, x) = Φ₂(g, Ax), or equivalently, one has the following commutative diagrams:

where σ_A(B) = ABA⁻¹ for B ∈ GL(V₁).

4. For a given G-space X, we shall use G_x to denote the isotropy subgroup of a point x and use G(x) to denote the orbit of x, namely

It is clear that G_g·x = gG_xg⁻¹ and the map g → g · x induces a bijection of G/G_x onto G(x).

Definitions 1. A (linear) subspace U of a given linear G-space V is called an invariant (or G-) subspace, if

2. A linear G-space V (or its corresponding representation of G on V) is said to be irreducible if {0} and V are the only invariant subspaces.

3. A linear G-space V (or its corresponding representation of G on V) is called completely reducible if it can be expressed as the direct sum of irreducible G-subspaces.

4. The following equations define the induced linear G-space structures of two given linear G-spaces V and W.

(i)direct sum: V ⊕ W with g · (x, y) = (gx, gy).

(ii)dual space: V^∗ with ⟨x, g · x′⟩ = ⟨g⁻¹ · x, x′⟩. (Notice that the inverse in the above definition is needed to ensure that ⟨x, g₁ · (g₂ · x′)⟩ = ⟨...

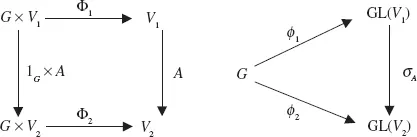
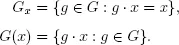
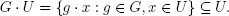
Table of contents

• Cover Page
• Series on University Mathematics
• Title
• Copyright
• Contents
• Preface
• Lecture 1 Linear Groups and Linear Representations
• Lecture 2 Lie Groups and Lie Algebras
• Lecture 3 Orbital Geometry of the Adjoint Action
• Lecture 4 Coxeter Groups, Weyl Reduction and Weyl Formulas
• Lecture 5 Structural Theory of Compact Lie Algebras
• Lecture 6 Classification Theory of Compact Lie Algebras and Compact Connected Lie Groups
• Lecture 7 Basic Structural Theory of Lie Algebras
• Lecture 8 Classification Theory of Complex Semi-Simple Lie Algebras
• Lecture 9 Lie Groups and Symmetric Spaces, the Classification of Real Semi-Simple Lie Algebras and Symmetric Spaces