Differential Geometry of Curves and Surfaces

0

Masaaki Umehara, Kotaro Yamada

• Publisher: WSPC
• Year: 2017
• eBook ISBN: 9789814740265
• Topic: Mathematics
• Subtopic: Differential Geometry
• Index: Mathematics

This engrossing volume on curve and surface theories is the result of many years of experience the authors have had with teaching the most essential aspects of this subject. The first half of the text is suitable for a university-level course, without the need for referencing other texts, as it is completely self-contained. More advanced material in the second half of the book, including appendices, also serves more experienced students well. Furthermore, this text is also suitable for a seminar for graduate students, and for self-study. It is written in a robust style that gives the student the opportunity to continue his study at a higher level beyond what a course would usually offer. Further material is included, for example, closed curves, enveloping curves, curves of constant width, the fundamental theorem of surface theory, constant mean curvature surfaces, and existence of curvature line coordinates. Surface theory from the viewpoint of manifolds theory is explained, and encompasses higher level material that is useful for the more advanced student. This includes, but is not limited to, indices of umbilics, properties of cycloids, existence of conformal coordinates, and characterizing conditions for singularities. In summary, this textbook succeeds in elucidating detailed explanations of fundamental material, where the most essential basic notions stand out clearly, but does not shy away from the more advanced topics needed for research in this field. It provides a large collection of mathematically rich supporting topics. Thus, it is an ideal first textbook in this field.

Chapter III

Surfaces from the Viewpoint of Manifolds*

In the previous chapters, we studied curves and surfaces, but looking at surfaces from the viewpoint of manifolds allows us to obtain a broader perspective. In this chapter, for those readers that are familiar with manifolds, we aim at the Hopf theorem (Theorem 17.4) for constant mean curvature surfaces, and continue with further study of surfaces. We start in Section 12 with a review of differential forms, and use them in Sections 13 and 14 to prove the Gauss-Bonnet theorem on 2-dimensional Riemannian manifolds. As an application of that, in Section 15 we prove the index formula for vector fields on compact oriented 2-manifolds and study the index of umbilics on a surface. In Section 16, we show existence of conformal coordinates for surfaces. Then in Section 17, we introduce the Gauss and Codazzi equations, and the fundamental theorem of surface theory, which will be proven in Appendix B.10, and prove the Hopf theorem. In Section 18, we explain the maximal speed descent property (the property of brachistocrones) for cycloids from the viewpoint of Riemannian geometry. Finally in Section 19, we give a proof of existence of geodesic triangulations on surfaces. In this chapter, we assume that the reader is familiar with vector fields on manifolds, differential forms, wedge products and exterior derivatives. (See the references suggested in the text within this chapter.)

12.Differential forms

We now assume the reader is familiar with manifolds, for example, the knowledge in Chapter 5 of Singer-Thorpe [35].

We will refer to the sets of real-valued differential 0-forms, 1-forms, 2-forms on a 2-manifold (i.e. 2-dimensional differentiable manifold) S as

⁰(S),

¹(S),

²(S), respectively. In fact,

⁰(S) is the same as the set C^∞(S) of smooth functions on S. The exterior derivative operators are linear maps between these sets as follows:

In particular, d₀ is the same as the exterior derivative d defined in Section 7.

Let

^∞(S) denote the set of all smooth vector fields on a manifold S. Then a differential 1-form is a linear map α:

^∞(S) → C^∞(S) that satisfies

A differential 2-form β, or 2-form β for short, satisfies

and so is a bilinear map β:

^∞(S) ×

^∞(S) → C^∞(S). Furthermore, when α and β are 1-forms, we can define their wedge product, or exterior product, “α ∧ β” as

(In some textbooks, the wedge produ...

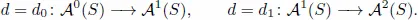
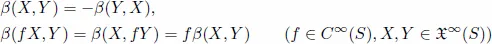
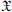
Table of contents

• Cover Page
• Title
• Copyright
• Contents
• Preface
• I. Curves
• II. Surfaces
• III. Surfaces from the Viewpoint of Manifolds*
• Appendix A Supplements
• Appendix B Advanced Topics on Curves and Surfaces
• Answers to Exercises
• Bibliography
• List of Symbols
• Index