A Guide to Mathematical Methods for Physicists

With Problems and Solutions

Michela Petrini, Gianfranco Pradisi, Alberto Zaffaroni

• Publisher: WSPC (EUROPE)
• Year: 2017
• eBook ISBN: 9781786343468
• Topic: Physical Sciences
• Subtopic: Mathematical & Computational Physics

-->

Mathematics plays a fundamental role in the formulation of physical theories. This textbook provides a self-contained and rigorous presentation of the main mathematical tools needed in many fields of Physics, both classical and quantum. It covers topics treated in mathematics courses for final-year undergraduate and graduate physics programmes, including complex function: distributions, Fourier analysis, linear operators, Hilbert spaces and eigenvalue problems. The different topics are organised into two main parts — complex analysis and vector spaces — in order to stress how seemingly different mathematical tools, for instance the Fourier transform, eigenvalue problems or special functions, are all deeply interconnected. Also contained within each chapter are fully worked examples, problems and detailed solutions.

A companion volume covering more advanced topics that enlarge and deepen those treated here is also available.

--> Contents:

• Complex Analysis:
  • Holomorphic Functions
  • Integration
  • Taylor and Laurent Series
  • Residues
• Functional Spaces:
  • Vector Spaces
  • Spaces of Functions
  • Distributions
  • Fourier Analysis
  • Linear Operators in Hilbert Spaces I: The Finite-Dimensional Case
  • Linear Operators in Hilbert Spaces II: The Infinite-Dimensional Case
• Appendices:
  • Complex Numbers, Series and Integrals
  • Solutions of the Exercises

-->
--> Readership: Students of undergraduate mathematics and postgraduate students of physics or engineering. -->
Complex Functions;Fourier Analysis;Hilbert Spaces;Eigenvalue Problems;Classical Physics;Quantum Physics;Methmatical Methods0 Key Features:

• Chosen topics are treated in depth, always keeping in mind physical applications and practical aspects
• Contains many examples and exercises with solutions for practical use for the students, emphasizing the main purpose of relating concrete physical examples with more formal mathematical aspects

PART I

Complex Analysis

1

Holomorphic Functions

The theory of complex functions is one of the most fascinating fields of analysis and is also an essential tool for theoretical physics. The idea is to extend to the functions of complex variable properties and theorems valid for real analysis. In particular, the aim is to define the notion of derivability and integrability of a function of complex variables. This will lead to the definition of holomorphic functions. We will discover that differentiability in complex sense is stronger than in real sense. In particular, functions that are differentiable once in complex sense are also infinitely differentiable and analytic.

1.1.Complex Functions

A function of complex variable is a map f : C → C that associates with each point z of the complex plane C (or a subset of it) one point of the same plane

Since f(z) is a complex number, we introduce its real and imaginary parts as follows:

where z = x + iy, and X(x, y) and Y(x, y) are real functions of the two real variables (x, y).

A first notion one can introduce is continuity. A function f(z) is continuous at a point z₀ if it is defined in a neighbourhood of z₀ and if

The limit is defined in analogy with the case of a function of one real variable: f(z₀) is the limit of f(z) for z → z₀ if, for any

> 0, there exists δ > 0 such that

Note however that we are taking the limit in a plane. Thus, as for functions of several real variables, the limit must be independent of the path chosen to approach z₀.

Example 1.1. The limit

does not exist, since it depends on the path in the complex plane chosen to approach z = 0. For instance, if we approach z = 0 along the real axis, z =

= x, while along the imaginary axis z = −

= iy. Thus, the limits take different values

From (1.2), it follows that, if a function f(z) is continuous at z₀ = x₀ + iy₀, its real and imaginary parts are also continuous at the point (x₀, y₀) of R². Similarly, one can show that the modulus of f,

is also continuous at z = z₀. Moreover, if the functions f(z) and g(z) are continuous at z = z₀, and h is continuous in g(z₀), then

are also continuous at z = z₀.

Given the notion of continuity at a point, one can extend it to continuity on a region of the complex plane. Let us first define a domain of the complex plane as an open, connected region of C. A function f(z) is said to be continuous on a domain D ⊆ C if it is continuous at each point of the domain. All the properties mentioned above hold on D.

Given a function f : D → C that associates to any z ∈ D a value w = f(z), one can define its inverse as

Strictly speaking, only injective functions admit an inverse. In complex analysis it is sometimes useful to define the inverse also for non-injective functions, but, in this case, f⁻¹(w) is not a function in the proper sense, since it associates multiple v...

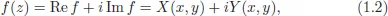
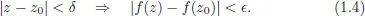
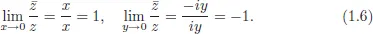
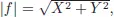
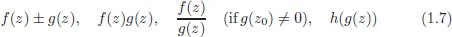
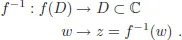
Table of contents

• Cover
• Halftitle
• Essential Textbooks in Physics
• Title
• Copyright
• Preface
• Contents
• PART I. Complex Analysis
• PART II. Functional Spaces
• PART III. Appendices
• Bibliography
• Index