Mathematics of Planet Earth

A Primer

Jochen Bröcker, Ben Calderhead;Davoud Cheraghi;Colin Cotter;Darryl HolmTobias KunaBeatrice PelloniTed ShepherdHilary Weller

• Publisher: WSPC (EUROPE)
• Year: 2017
• eBook ISBN: 9781786343857
• Topic: Mathematics
• Subtopic: Applied Mathematics
• Index: Mathematics

-->

Mathematics of Planet Earth (MPE) was started and continues to be consolidated as a collaboration of mathematical science organisations around the world. These organisations work together to tackle global environmental, social and economic problems using mathematics.

This textbook introduces the fundamental topics of MPE to advanced undergraduate and graduate students in mathematics, physics and engineering while explaining their modern usages and operational connections. In particular, it discusses the links between partial differential equations, data assimilation, dynamical systems, mathematical modelling and numerical simulations and applies them to insightful examples.

The text also complements advanced courses in geophysical fluid dynamics (GFD) for meteorology, atmospheric science and oceanography. It links the fundamental scientific topics of GFD with their potential usage in applications of climate change and weather variability. The immediacy of examples provides an excellent introduction for experienced researchers interested in learning the scope and primary concepts of MPE.

-->

Request Inspection Copy

--> Contents:

• Foreword
• Introduction
• The General Circulation of the Atmosphere and Oceans (Theodore G Shepherd)
• Partial Differential Equations (Beatrice Pelloni and Darryl Holm)
• Data and Probability (Jochen Bröcker and Ben Calderhead)
• Dynamical Systems (Davoud Cheraghi and Tobias Kuna)
• Numerical Methods (Colin Cotter and Hilary Weller)
• Bibliography
• Index

-->
--> Readership: Advanced undergraduate and graduate students in mathematics, physics and engineering; advanced students of geophysical fluid dynamics (GFD) for meteorology, atmospheric science and oceanography. -->
Mathematics of Planet Earth;Partial Differential Equations;Data Assimilation;Dynamical Systems;Mathematical Modelling;Numerical Simulations;Geophysical Fluid Dynamics;GFD0

Chapter 1

The General Circulation of the Atmosphere and Oceans

Theodore G. Shepherd

University of Reading, UK

1.1 Introduction

The goal of this chapter is to show how many of the key observed features of the general circulation of the atmosphere and oceans may be explained from the fundamental physical constraints that are represented mathematically in the governing equations. Most of the emphasis is on aspects of climate, meaning the time-averaged behaviour of the system (including higher-order moments such as correlations of fluctuations), but some discussion is also provided of atmospheric weather systems, meaning the dayto-day variations of the state of the atmosphere. The observed features are explained through the simplest possible mathematical model of the relevant physical processes, and there are many connections to the PDE models of geophysical fluid dynamics discussed in Chapter 2.

Analytical solutions of the governing equations are restricted to a few very special cases, and even the simplest dynamical models can generally only be solved numerically (Chapter 5). Also, comparisons between models and observations, as well as the predictability of weather, raise issues of probability and representativeness (Chapter 3), whilst systemlevel (or emergent) behaviour requires understanding of dynamical systems (Chapter 4). None of that is touched upon in this chapter.

It is rather remarkable how such crucial aspects of the general circulation as tropical rain belts, deserts, storm tracks, coastal upwelling regions (important for fisheries), and western oceanic boundary currents — also westerly and easterly surface winds, which used to be enormously important in the days of sailing ships — can be explained in a qualitative way from basic physical principles. This is the basis of the concept of using a hierarchy of models to represent the atmosphere and oceans. By including more detailed mathematical representations of the relevant physical processes, the model solutions can be expected to become more quantitatively accurate. Nevertheless, the essential causal relationships are represented in the simplest models, and these are often the basis of diagnostic theories that are used to understand the workings of the more complex models, such as those used for operational weather and climate prediction.

Some thoughts are also provided at the end of this chapter concerning what can be said about climate change. Here, the difference between qualitative and quantitative understanding becomes crucial.

1.2 Zonally Integrated View of Atmospheric and Oceanic Circulation

The atmosphere and oceans obey the laws of fluid dynamics, represented by the Navier–Stokes equations which express conservation of energy, momentum, and mass (see Chapter 2, Sec. 2.2 for the incompressible case, and Chapter 5, Sec. 5.1 for the compressible case). For the atmosphere, these are complemented by a conservation law for moisture. The steady forms of these conservation laws represent physical balances, and much can be deduced about the circulation from them. It is convenient to start by considering the zonally (or longitudinally) integrated balances.

1.2.1 Energy balance

Because the Earth is approximately spherical, incident solar radiation is approximately proportional to the cosine of latitude, modulated by the seasonal cycle. Hence, most solar radiation is absorbed in the tropics. The outgoing longwave radiation (OLR), which depends on atmospheric temperature according to the Stefan–Boltzmann (blackbody radiation) law, is also greatest in the tropics because that is where temperatures are highest, but the equator-to-pole contrast in OLR is weaker than that in the absorbed solar radiation (ASR). Overall, the net OLR must balance the ASR, otherwise the atmospheric temperature adjusts to make it so. As a result, there is a net heating of the climate system in the tropics (ASR > OLR), where temperatures are relatively high, and a net cooling in the higher latitudes (OLR > ASR), where temperatures are relatively low (Fig. 1.1). Conservation of energy implies a downgradient transfer of energy by the climate system from the tropics to higher latitudes. Indeed the second law of thermodynamics implies that it must be this way.

Figure 1.1. Energy balance of the climate system as a function of latitude. The emission of terrestrial radiation is the OLR, and the incoming solar energy is the ASR. Reproduced with permission from Suomi virtual museum, University of Wisconsin-Madison (http://profhorn.meteor.wisc.edu/wxwise/museum/a2main.html).

Observations show that most of this poleward energy transport is accomplished by the atmosphere. The oceanic heat transport is important regionally, and for the time evolution of climate (since the heat capacity of the oceans is much greater than that of the atmosphere), but it can be ignored for a basic understanding of the energy balance of the climate system. Thus, the rest of Sec. 1.2 focuses on the atmosphere.

There is also a vertical transfer of energy within the atmosphere, because most of the ASR is absorbed at the Earth’s surface, whilst the longwave emission to space occurs from the atmosphere itself (Fig. 1.2). This is because the atmosphere is largely transparent to solar radiation but opaque to longwave radiation. The latter property is what gives rise to the greenhouse effect (Sec. 1.6). Because the atmosphere is heated from below and cooled from above, it undergoes convective instability (much as soup heated on a stove), which leads to turbulent heat transport. In contrast, the ocean is heated from above so it is not subject to spontaneous instability; its motion is mainly forced mechanically, by the atmosphere (Sec. 1.3).

Figure 1.2. The energy balance of the climate system. Most of the solar radiation that is not reflected is absorbed at Earth’s surface. But most of the OLR is emitted from the atmosphere itself. This gives rise to the greenhouse effect. Reproduced from Intergovernme...

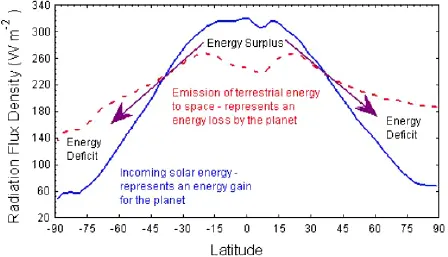
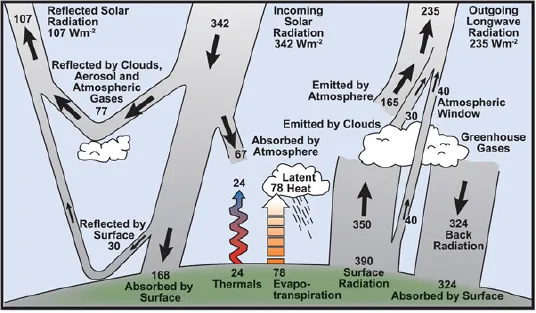
Table of contents

• Cover page
• Title page
• Copyright
• Foreword
• Introduction
• Contents
• 1. The General Circulation of the Atmosphere and Oceans
• 2. Partial Differential Equations
• 3. Data and Probability
• 4. Dynamical Systems
• 5. Numerical Methods
• Bibliography
• Index