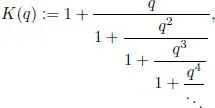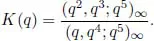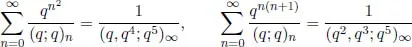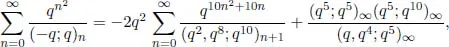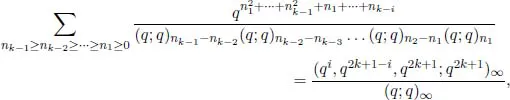Topics and Methods in q-Series

James Mc Laughlin

• Publisher: WSPC
• Year: 2017
• ISBN:
  9789813223387
• Topic: Matemáticas
• Subtopic: Análisis funcional

-->

The book provides a comprehensive introduction to the many aspects of the subject of basic hypergeometric series. The book essentially assumes no prior knowledge but eventually provides a comprehensive introduction to many important topics. After developing a treatment of historically important topics such as the q-binomial theorem, Heine's transformation, the Jacobi triple product identity, Ramanujan's 1-psi-1 summation formula, Bailey's 6-psi-6 summation formula and the Rogers-Fine identity, the book goes on to delve more deeply into important topics such as Bailey- and WP-Bailey pairs and chains, q-continued fractions, and mock theta functions. There are also chapters on other topics such as Lambert series and combinatorial proofs of basic hypergeometric identities.

The book could serve as a textbook for the subject at the graduate level and as a textbook for a topic course at the undergraduate level (earlier chapters). It could also serve as a reference work for researchers in the area.

--> Contents:

• Foreword
• Introduction
• Basic Notation
• The q -Binomial Theorem
• Heine's Transformation
• Other Important Basic Hypergeometric Transformations
• The Jacobi Triple Product Identity
• Ramanujan's 1 ψ 1 Summation Formula
• Bailey's 6 ψ 6 Summation
• The Rogers–Fine Identity
• Bailey Pairs
• Bailey Chains
• WP-Bailey Pairs and Chains
• Further Results on Bailey/WP-Bailey Pairs and Chains
• Gaussian Polynomials
• Bijective Proofs of Basic Hypergeometric Identities
• q -Continued Fractions
• Lambert Series
• Mock Theta Functions
• Appendices:
  • Frequently Used Theorems
  • WP-Bailey Chains
  • WP-Bailey Pairs
  • Bailey Chains
  • Bailey Pairs
  • Mock Theta Functions
  • Selected Summation Formulae
• Bibliography
• Author Index
• Subject Index

-->
--> Readership: Undergraduate and graduate students. -->
Keywords:q-Series;Basic Hypergeometric Series;Bailey Pairs;WP-bailey Pairs;Mock Theta Functions;Rogers-Ramanujan Type Identities;q-Continued FractionsReview: Key Features:

• The book is essentially self-contained, all the pre-requisites are essentially covered in earlier chapters of the book
• There is a comprehensive selection of guided exercises at the end of each chapter, allowing the reader to go deeper into the subject, and permitting the book to be used both as a graduate text book, and an undergraduate text book for a topics course
• No other book that treats the same or nearby subjects is as accessible to a reader as this one, nor does any such book cover the same selection of topics

Chapter 1

Introduction

I first encountered the subject of basic hypergeometric series while attending the weekly analytic number theory seminar in the mathematics department at the University of Illinois at Urbana-Champaign (UIUC). I was a graduate student there from 1996 to 2002, and the weekly seminars were something that I looked forward to every week. It was in these seminars that I first heard of such mathematical objects as q-series, mock theta functions, partition congruences and partition identities, infinite q-series-product identities, q-continued fractions, and the fascinating mathematics of Ramanujan. All of these objects were to eventually develop into long-term mathematical interests of my own, and to become important to me in my own research.

At the start of my graduate studies, one of my interests was the regular continued fraction expansions of real numbers (Pell’s equation, patterns in the expansion of powers of e, folding patterns in the expansion of various infinite products, etc.), and I had some vague idea of doing some research in the area of continued fractions for my thesis topic. Thus, while not being a regular continued fraction, an immediate object of interest was the Rogers-Ramanujan continued fraction (and later other q-continued fractions of Ramanujan, Gordon, Selberg and others). One of the interesting facts about the Rogers-Ramanujan continued fraction

is that, for |q| < 1, it has a representation as a quotient of infinite products:

Of course the famous Rogers-Ramanujan identities

mean that K(q) also has a representation as a quotient of basic hypergeometric series. The Rogers-Ramanujan identities were just two examples from a list of 130 similar identities stated and proved by Lucy Slater in two papers [236, 237] published in 1951 and 1952. The Rogers-Ramanujan identities, and indeed Slater’s entire compendium of such identities, were a mystery to me at the time, and trying to understand the mechanism of the proofs would eventually lead me into the extensive mathematical area involving Bailey pairs, WP-Bailey pairs and Bailey- and WP-Bailey chains and trees.

Another group of mysterious objects that cropped up from time to time in talks that I attended were the mock theta functions. Of course Zwegers [263, 264] has given an explanation of the mock theta functions in terms of Maass forms, but when I first saw examples of the q-series representations of mock theta functions, the only observation I could make was the trivial one that n-th terms of these series were all lacking a term of the form (q; q)_n (or (q^k; q^k)_n) in the denominator (unlike all of the basic hypergeometric series in all of the usual q-series identities that I was aware of). This was one small reason, amongst the many deeper reasons, that the identities comprising the mock theta conjectures, for example that if |q| < 1, then

seemed like very strange beasts indeed! I was still curious enough about the mock theta functions to want to understand more about their basic hypergeometric nature.

However, I did not really start to study q-series in their own right (as opposed to regarding them as having connections with q-continued fractions) until several years later. I continued to work in the area of continued fractions. Doug Bowman, who I knew was interested in continued fractions, became my thesis advisor, and I defended my thesis in May 2002 (the topic related to the convergence behavior of q-continued fractions, such as the Rogers-Ramanujan continued fraction, on the unit circle, at points which were not roots of unity).

I took up a visiting position at Trinity College, in Hartford, Ct, with the aim of continuing my research on continued fractions, collaborating with Nancy Wyshinski at Trinity, whose interests lay in the analytic theory of continued fractions. I continued to work almost entirely in the broad field of continued fractions up until around 2008, when I got interested in the area of basic hypergeometric series again, when trying to prove some identities I had found experimentally, via a computer search. Since then, my primary research interests have generally moved over to the broad field of q-series.

As I read deeper, I discovered many interesting methods for proving basic hypergeometric identities that had appeared during the last 50 or so years. Many new interesting mathematical objects had likewise appeared in the field of q-series, and our understanding of many classical objects has also developed.

Examples of the new methods and techniques (or in some cases, new applications of existing methods and techniques) included the anti-telescoping method of Andrews, Cauchy augmentation, applications of the Cauchy differential operator, q-Lagrange inversion, matrix inverse methods, the WZ-method and the q-Zeilberger algorithm, applications of Abel summation, q-Engel expansion of q-functions, etc.

Apart from the development of new methods to prove q-series identities, other developments in the field include the connection between mock theta functions and Maass forms made by Zwegers, elliptic hypergeometric functions, many developments in the topics of Bailey- and WP-Bailey pairs and chains/lattices, various classes of multi-sum identities such as the Andrews-Gordon identities

explicit formulae for radial limits for many of the mock theta functions, congruence relations (and other properties) for the generating functions of new partition functions (the crank, overpartitions, smallest parts function, etc.), various polynomial versions of Slater-type identities, m-versions of Slater-type identities, new modular relations for various q-functions, multi-sectioning of various infinite products, and many others.

Most of these results were scattered throughout the mathematical literature, and as time went on, the thought grew that it would be good to bring many of these developments together and present them in a way that would be accessible to beginners in the field. That idea was the original motivation for this book.¹

The book starts with the basics, and Chapters 2–8 cover what might be described as classical material in the subject, namely, the q-binomial theorem, Heine’s transformation and various summations that derive from it, transformations of Watson (₈ϕ₇) and Bailey (₁₀ϕ₉), the Jacobi triple product identity, Ramanujan’s ₁ψ₁ summation and Bailey’s ₆ψ₆ summation. These chapters, with perhaps a selection of topics from Chapter 9 (the Rogers-Fine Identity), Chapter 10 (Bailey Pairs), Chapter 14 (Gaussian Polynomials), Chapter 15 (Bijective Proofs) and Chapter 17 (Lambert Series), could easily provide material for an undergraduate topics course. Every chapter has an extensive selection of exercises.

The remainder of the book contains an extensive treatment of many aspects of Bailey- and WP-Bailey pairs and chains in Chapters 11–13, a quite comprehensive introduction to q-continued fractions in Chapter 16, and an introduction to the mock theta functions in Chapter 18. The book can also serve as a text for a graduate course, the selection of topics beyond the basic ones being up to the instructor.

I have tried to keep the book as self-contained as possible. Apart from some general convergence theorems for continued fractions needed to ensure the convergence of certain q-continued fractions, and which are just quoted, a newcomer to the topic who had the equivalent of an undergraduate course in analysis, and who was prepared to work through the mathematics in the text and the exercises, should be able work their way through most, possibly all, of the book.

I believe the text can also serve as a reference work for researchers in the area. The text includes many results from the literature, both as examples in the text and as exercises at the end of each chapter.

I would like to thank a number of people who were very helpful in bringing this book to completion. At World Scientific, I would like to express deep thanks and appreciation to Rochelle Kronzek for her help, enthusiasm and encouragement all the way through this project. I would also like to thank Bruce Berndt for adopting the book to be part of the Monographs in Number Theory series, of which he is the series editor. A big thank you is due to George Andrews for agreeing to write a preface for the book, and for the kind remarks he made about the text. Thanks also to Krishna Alladi and Tim Huber who looked at earlier drafts of the manuscript and encouraged me to complete it.

I would also like to take this opportunity to look back in time and thank all my co-authors on papers we wrote together on q-series, and who made the paper-writing process more interesting and enjoyable — (in chronological order) Doug Bowman, Nancy Wyshinski, Andrew Sills, Peter Zimmer, Dennis Eichhorn, Scott Parsell, Jongsil Lee and Jaebum Sohn. I would also like to thank Doug Bowman, who was my thesis advisor when I was a graduate student and also a lot of fun to hang out with and sink a few beers with. Thanks also to some of my former professors at the University of Illinois at Urbana-Champaign, who made my time as a graduate student such an interesting and enjoyable experience — (in alphabetical order) Michael Bennett, Bruce Berndt, Nigel Boston, Harold Diamond, Adolf Hildebrand, Bruce Reznick, Ken Stolarsky and Alexandru Zaharescu. My apologies to anyone that I should have thanked and have forgotten.

A significant part of this book was written while on sabbatical from teaching at West Chester University in Fall 2014. I am very appreciative of the un-interrupted time this sabbatical gave me to concentrate on writing the book. The book may not have happened, or at least would have taken considerably longer, without this sabbatical.

Lastly, I would like to thank my wife Julie for putting up with the various inconveniences caused by the writing of this book, and also for putting up with all the times that I have woken her up talking mathematics in my sleep (including the time she says I was ranting about “… zeros as far as the eye could see … ”).

Exton, PA.
February 2017.

Remark: Despite the best efforts of the author, and others involved in the editing/proofreading process, some typographical errors may have slipped by. These are solely the fault of the author. Any such errors found after the publication of the book will be posted on the “errata page” for the book at http://www.worldscientific...