Probability and Random Number

A First Guide to Randomness

Hiroshi Sugita

• Publisher: WSPC
• Year: 2017
• eBook ISBN: 9789813228276
• Topic: Mathematics
• Subtopic: Computer Science General
• Index: Mathematics

-->

This is a book of elementary probability theory that includes a chapter on algorithmic randomness. It rigorously presents definitions and theorems in computation theory, and explains the meanings of the theorems by comparing them with mechanisms of the computer, which is very effective in the current computer age.

Random number topics have not been treated by any books on probability theory, only some books on computation theory. However, the notion of random number is necessary for understanding the essential relation between probability and randomness. The field of probability has changed very much, thus this book will make and leave a big impact even to expert probabilists.

Readers from applied sciences will benefit from this book because it presents a very proper foundation of the Monte Carlo method with practical solutions, keeping the technical level no higher than 1st year university calculus.

--> Contents:

• Mathematics of Coin Tossing
  • Mathematical Model
  • Random Number
  • Limit Theorem
  • Monte Carlo Method
  • Infinite coin Tosses
• Random Number:
  • Recursive Function
  • Kolmogorov Complexity and Random Number
• Limit Theorem:
  • Bernoulli's Theorem
  • Law of Large Numbers
  • De Moivre–Laplace's Theorem
  • Central Limit Theorem
  • Mathematical Statistics
• Monte Carlo Method:
  • Monte Carlo Method as Gambling
  • Pseudorandom Generator
  • Monte Carlo Integration
  • From the Viewpoint of Mathematical Statistics
• Appendices:
• • Symbols and Terms
  • Binary Numeral System
  • Limit of Sequence and Function
  • Limits of Exponential Function and Logarithm
  • C Language Program

-->
--> Readership: First year university students to professionals. -->
Keywords:Probability;Probability Theory;Randomness;Random Number;Pseudorandom Number;Monte Carlo Method;Monte Carlo IntegrationReview: Key Features:

• This is the first book that presents both probability theory and algorithmic randomness for from 1st year university students to experts. It is technically easy but worth reading for experts as well
• This book presents basic limit theorems with proofs that are not seen in usual probability textbooks; for readers should learn that a good solution is not always unique
• This book rigorously treats the Monte Carlo method. In particular, it presents the random Weyl sampling, which produces pseudorandom numbers for the Monte Carlo integration that act complete substitutes for random numbers

Chapter 1

Mathematics of coin tossing

Tossing a coin many times, record 1 if it comes up Heads and record 0 if it comes up Tails at each coin toss. Then, we get a long sequence consisting of 0 and 1—let us call such a sequence a {0, 1}-sequence—that is random. In this chapter, with such random {0, 1}-sequences as material, we study outlines of

•how to describe randomness (Sec. 1.1),

•how to define randomness (Sec. 1.2),

•how to analyze randomness (Sec. 1.3.1), and

•how to make use of randomness (Sec. 1.3.2, Sec. 1.4).

Readers may think that coin tosses are too simple as a random object, but as a matter of fact, virtually all random objects can be mathematically constructed from them (Sec. 1.5.2). Thus analyzing coin tosses means analyzing all random objects.

In this chapter, we present only basic ideas, and do not prove theorems.

1.1Mathematical model

For example, the concept ‘circle’ is obtained by abstracting an essence from various round objects in the world. To deal with circle in mathematics, we consider an equation (x − a)² + (y − b)² = c² as a mathematical model. Namely, what we call a circle in mathematics is the set of all solutions of this equation

{(x, y) | (x − a)² + (y − b)² = c²}.

Similarly, to analyze random objects, since we cannot deal with them directly in mathematics, we consider their mathematical models. For example, when we say ‘n coin tosses’, it does not mean that we toss a real coin n times, but it means a mathematical model of it, which is described by mathematical expressions in the same way as ‘circle’.

Let us consider a mathematical model of ‘3 coin tosses’. Let X_i ∈ {0, 1} be the outcome (Heads = 1 and Tails = 0) of the i-th coin toss. At high school, students learn the probability that the consecutive outcomes of 3 coin tosses are Heads, Tails, Heads, is

Here, however, the mathematical definitions of P and X_i are not clear. After making them clear, we can call them a mathematical model of 3 coin tosses.

Fig. 1.1 Heads and Tails of 1 JPY coin

Example 1.1. Let {0, 1}³ denote the set of all {0, 1}-sequences of length 3:

Let

({0, 1}³) be the power set^†1 of {0, 1}³, i.e., the set of all subsets of {0, 1}³. A ∈

({0, 1}³) is equivalent to A ⊂ {0, 1}³. Let #A denote the number of elements of A. Now, define a function

by

(See Definition A.2), and functions ξ_i : {0, 1}³ → {0, 1}, i = 1, 2, 3, by

Each ξ_i is called a coordinate function. Then, we have

Although (1.3) has nothing to do with the real coin tosses, it is formally the same as (1.1). Readers can easily examine the formal identity not only for the case Heads, Tails, Heads, but also for any other possible outcomes of 3 coin tosses. Thus we can compute every probability concerning 3 coin tosses by using P₃ and

. This means that P and

in (1.1) can be considered as P₃ and

, respectively. In other words, by the correspondence

P₃ and

are a mathematical model of 3 coin tosses.

The equation (x − a)² + (y − b)² = c² is not a unique mathematica...

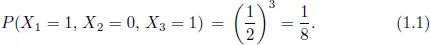
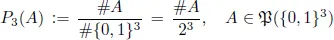
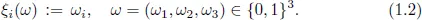
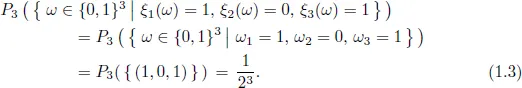
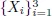
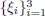
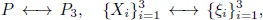
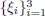
Table of contents

• Cover Page
• Title
• Copyright
• Preface
• Contents
• 1. Mathematics of coin tossing
• 2. Random number
• 3. Limit theorem
• 4. Monte Carlo method
• Appendix A
• List of mathematicians
• Further reading
• Bibliography
• Index