Quantum States and Scattering in Semiconductor Nanostructures

Camille Ndebeka-Bandou, Francesca Carosella;Gérald Bastard

• Publisher: WSPC (EUROPE)
• Year: 2017
• eBook ISBN: 9781786343048
• Topic: Physical Sciences
• Subtopic: Condensed Matter

-->

This book is an introduction to quantum states and of their scattering in semiconductor nanostructures. Written with exercises and detailed solutions, it is designed to enable readers to start modelling actual electron states and scattering in nanostructures. It first looks at practical aspects of quantum states and emphasises the variational and perturbation approaches. Following this there is analysis of quasi two-dimensional materials, including discussion of the eigenstates of nanostructures, scattering mechanisms and their numerical results.

Focussing on practical applications, this book moves away from standard discourse on theory and provides students of physics, nanotechnology and materials science with the opportunity to fully understand the electronic properties of nanostructures.

--> Headers: With more than 50 Exercises & Solutions (168 pages)
Contents:

• Practical Quantum Mechanics:
  • Schrödinger Equation
  • Bound and Extended States
  • Approximate Methods
  • Landau Quantisation of Electron Motion in Ideal Semiconductor Bulks and Heterostructures
• The Physics of Heterostructures:
  • Background on Heterostructures
  • Electrons States in Nanostructures
  • Beyond the Ideal World
  • Screening at the Semi-Classical Approximation
  • Results for Static Scatterers
  • Results for Electron-Phonon Interaction
  • Beyond the Born Approximation
• Exercises

-->
--> Readership: Students of physics, nanoscience and materials science, professionals working with nanomaterials, and researchers. -->
Keywords:Nanostructures;2D Structures;Laser;Carriers;Heterostructures;Quantum Mechanics;Perturbation Theory; Fermi Golden Rule;Screening;Scattering;Impurities;PhononsReview:

"This book teaches how to solve many important problems analytically. 253 pages of well-structured text is complemented by 165 pages of more than 50 exercises. I recommend it to all who seek understanding and insight."

Prof Dieter Bimberg
Technical University of Berlin
0

PART I

Practical Quantum Mechanics

Chapter I.1

Schrödinger Equation

Classical mechanics states that the state of a physical system is described by the knowledge of the positions and velocities at time t plus the Newton (or Lagrange or Hamilton) law for its evolution.

Quantum mechanics states the following two rules for describing a physical system.

Rule 1. The space of any physical system is described by (state) vectors conventionally noted by |ψ⟩ that belong to a Hilbert space. A Hilbert space is an abstract vector space possessing the structure of an inner product: if |φ₁⟩ and |φ₂⟩ are two state vectors belonging to the Hilbert space, their inner product is:

where * denotes the complex conjugation. Hilbert spaces are complete (i.e., if every Cauchy sequence in M has a limit in M). They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis.

Rule 2. For non-relativistic particles, the time evolution of the state vectors is given by the Schrödinger equation:

where H is the Hamiltonian operator. For N particles, the Hamiltonian is the sum of the N kinetic energies and of the potential energies. The latter comprise the interactions U_i between the particles and external fields plus the particle–particle interactions V_ij:

where m_i is the mass of the ith particle.

While the quantum mechanical description is seldom useful for macroscopic bodies, it proves of paramount importance for very small objects (elementary particles, atoms, nano-objects) and thus for the understanding of the behaviour of many semiconductor devices.

Most of the times in this book we shall focus on the so-called position-representation where the state vector is projected on the

basis: for N particles this defines the N particles wavefunctions ψ(

₁,

₂, . . . ,

_N, t).

The physical interpretation of ψ(

₁,

₂, . . . ,

_N, t) is

which represents the probability to find at time t the first particle in an infinitesimal volume d³r₁ around

₁, the second particle in an infinitesimal volume d³r₂ around

₂, the Nth particle in an infinitesimal volume d³r_N around

_N. It results from this definition that the wavefunctions have to be normalised:

The N particles wavefunction ψ(

₁,

₂, . . . ,

_N, t) is the solution of the partial differential equation:

In the Hamiltonian function, one should replace the linear momentum

by −iħ

where

is the gradient operator:

Note that if the particles are identical, a special prescription will have to be made on the shape of ψ(

₁,

₂, . . . ,

_N, t). Rule of symmetrisation or antisymmetrisation of the wavefunctions depending on whether the identical particles are bosons (with integer spins) or fermions (with half integer spins) will be given:

If H is time independent, then |ψ(t)⟩ can be factorised:

In the

representation, this means that the wavefunction ψ(

₁,

₂, . . . ,

_N, t) can be factorised into the product of an t-dependent function by an

-dependent function. Inserting this ansatz into the Schrödinger equation, one finds readily that the wavefunction should be written:

In the equation H|φ⟩ = E|φ⟩, the vector |φ⟩ is such that applying H on it produces a vector that is proportional to it (in other word...

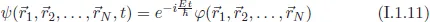
Table of contents

• Cover page
• Title page
• Contents
• Foreword
• About the Authors
• Part I Practical Quantum Mechanics
• Part II The Physics of Heterostructures
• Part III Exercises
• Bibliography
• Index