Quantum Techniques in Stochastic Mechanics

John Baez, Jacob D Biamonte

• Publisher: WSPC
• Year: 2018
• ISBN:
  9789813226968
• Topic: Physical Sciences
• Subtopic: Mechanics

-->

We introduce the theory of chemical reaction networks and their relation to stochastic Petri nets — important ways of modeling population biology and many other fields. We explain how techniques from quantum mechanics can be used to study these models. This relies on a profound and still mysterious analogy between quantum theory and probability theory, which we explore in detail. We also give a tour of key results concerning chemical reaction networks and Petri nets.

--> Contents:

• Stochastic Petri Nets
• The Rate Equation
• The Master Equation
• Probabilities vs Amplitudes
• Annihilation and Creation Operators
• An Example from Population Biology
• Feynman Diagrams
• The Anderson–Craciun–Kurtz Theorem
• An Example of the Anderson–Craciun–Kurtz Theorem
• A Stochastic Version of Noether's Theorem
• Quantum Mechanics vs Stochastic Mechanics
• Noether's Theorem: Quantum vs Stochastic
• Chemistry and the Desargues Graph
• Graph Laplacians
• Dirichlet Operators and Electrical Circuits
• Perron–Frobenius Theory
• The Deficiency Zero Theorem
• Example of the Deficiency Zero Theorem
• Example of the Anderson–Craciun–Kurtz Theorem
• The Deficiency of a Reaction Network
• Rewriting the Rate Equation
• The Rate Equation and Markov Processes
• Proof of the Deficiency Zero Theorem
• Noether's Theorem for Dirichlet Operators
• Computation and Petri Nets
• Summary Table

-->
--> Readership: Graduate students and researchers in the field of quantum and mathematical physics. -->
Keywords:Stochastic;Quantum;Markov Process;Chemical Reaction Network;Petri NetReview: Key Features:

• It's a light-hearted introduction to a deep analogy between probability theory and quantum theory
• It explains how stochastic Petri nets can be used in modeling in biology, chemistry, and many other fields
• It gives new proofs of some fundamental theorems about chemical reaction networks

Chapter 1 Stochastic Petri Nets

Stochastic Petri nets are one of many different diagrammatic languages people have evolved to study complex systems. We’ll see how they’re used in chemistry, molecular biology, population biology and queuing theory, which is roughly the science of waiting in line. Here’s an example of a Petri net taken from chemistry:

It shows some chemicals and some reactions involving these chemicals. To make it into a stochastic Petri net, we’d just label each reaction by a positive real number: the reaction rate constant, or Petri net for short.

Chemists often call different kinds of chemicals ‘species’. In general, a Petri net will have a set of species, which we’ll draw as yellow circles, and a set of transitions, which we’ll draw as blue rectangles. Here’s a Petri net from population biology:

Now, instead of different chemicals, the species really are different species of animals! And instead of chemical reactions, the transitions are processes involving these species. This Petri net has two species: rabbit and wolf. It has three transitions:

• In birth, one rabbit comes in and two go out. This is a caricature of reality: these bunnies reproduce asexually, splitting in two like amoebas.

• In predation, one wolf and one rabbit come in and two wolves go out. This is a caricature of how predators need to eat prey to reproduce. Biologists might use ‘biomass’ to make this sort of idea more precise: a certain amount of mass will go from being rabbit to being wolf.

• In death, one wolf comes in and nothing goes out. Note that we’re pretending rabbits don’t die unless they’re eaten by wolves.

If we labelled each transition with a number called a rate constant, we’d have a ‘stochastic’ Petri net.

To make this Petri net more realistic, we’d have to make it more complicated. We’re trying to explain general ideas here, not realistic models of specific situations. Nonetheless, this Petri net already leads to an interesting model of population dynamics: a special case of the so-called ‘Lotka–Volterra predatorprey model’. We’ll see the details soon.

More to the point, this Petri net illustrates some possibilities that our previous example neglected. Every transition has some ‘input’ species and some ‘output’ species. But a species can show up more than once as the output (or input) of some transition. And as we see in ‘death’, we can have a transition with no outputs (or inputs) at all.

But let’s stop beating around the bush, and give you the formal definitions. They’re simple enough:

Definition 1. A Petri net consists of a set S of species and a set T of transitions, together with a function

saying how many copies of each species shows up as input for each transition, and a function

saying how many times it shows up as output.

Definition 2. A stochastic Petri net is a Petri net together with a function

giving a rate constant for each transition.

Starting from any stochastic Petri net, we can get two things. First:

• The master equation. This says how the probability that we have a given number of things of each species changes with time.

Since stochastic means ‘random’, the master equation is what gives stochastic Petri nets their name. The master equation is the main thing we’ll be talking about in future chapters. But not right away!

Why not?

In chemistry, we typically have a huge number of things of each species. For example, a gram of water contains about 3 × 10²² water molecules, and a smaller but still enormous number of hydroxide ions (OH⁻), hydronium ions (H₃O⁺), and other scarier things. These things blunder around randomly, bump into each other, and sometimes react and turn into other things. There’s a stochastic Petri net describing all this, as we’ll eventually s...

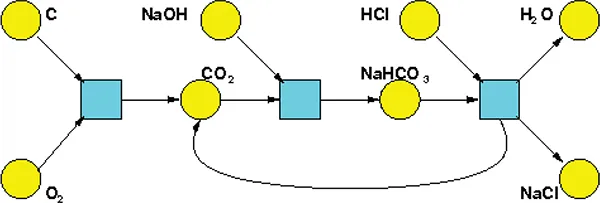
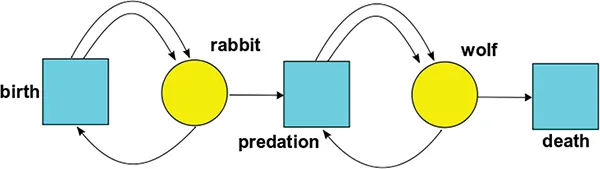
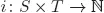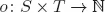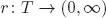Table of contents

• Cover
• Halftitle
• Title
• Copyright
• Preface
• Contents
• 1 Stochastic Petri Nets
• 2 The Rate Equation
• 3 The Master Equation
• 4 Probabilities vs Amplitudes
• 5 Annihilation and Creation Operators
• 6 An Example from Population Biology
• 7 Feynman Diagrams
• 8 The Anderson–Craciun–Kurtz Theorem
• 9 An Example of the Anderson–Craciun–Kurtz Theorem
• 10 A Stochastic Version of Noether’s Theorem
• 11 Quantum Mechanics vs Stochastic Mechanics
• 12 Noether’s Theorem: Quantum vs Stochastic
• 13 Chemistry and the Desargues Graph
• 14 Graph Laplacians
• 15 Dirichlet Operators and Electrical Circuits
• 16 Perron–Frobenius Theory
• 17 The Deficiency Zero Theorem
• 18 Example of the Deficiency Zero Theorem
• 19 Example of the Anderson–Craciun–Kurtz Theorem
• 20 The Deficiency of a Reaction Network
• 21 Rewriting the Rate Equation
• 22 The Rate Equation and Markov Processes
• 23 Proof of the Deficiency Zero Theorem
• Further Directions
• 24 Noether’s Theorem for Dirichlet Operators
• 25 Computation and Petri Nets
• 26 Summary Table
• Index