An Introduction to the Analysis of Algorithms

Michael Soltys

• Publisher: WSPC
• Year: 2018
• eBook ISBN: 9789813235922
• Edition: 3
• Topic: Computer Science
• Subtopic: Programming
• Index: Computer Science

-->

A successor to the first and second editions, this updated and revised book is a leading companion guide for students and engineers alike, specifically software engineers who design algorithms. While succinct, this edition is mathematically rigorous, covering the foundations for both computer scientists and mathematicians with interest in the algorithmic foundations of Computer Science.

Besides expositions on traditional algorithms such as Greedy, Dynamic Programming and Divide & Conquer, the book explores two classes of algorithms that are often overlooked in introductory textbooks: Randomised and Online algorithms — with emphasis placed on the algorithm itself. The book also covers algorithms in Linear Algebra, and the foundations of Computation.

The coverage of Randomized and Online algorithms is timely: the former have become ubiquitous due to the emergence of cryptography, while the latter are essential in numerous fields as diverse as operating systems and stock market predictions.

While being relatively short to ensure the essentiality of content, a strong focus has been placed on self-containment, introducing the idea of pre/post-conditions and loop invariants to readers of all backgrounds, as well as all the necessary mathematical foundations. The programming exercises in Python will be available on the web (see http://www.msoltys.com/book for the companion web site).

-->
--> Contents:

• Preliminaries
• Greedy Algorithms
• Divide and Conquer
• Dynamic Programming
• Online Algorithms
• Randomized Algorithms
• Algorithms in Linear Algebra
• Computational Foundations
• Mathematical Foundations

-->
--> Readership: Students of undergraduate courses in algorithms and programming and associated professionals. -->
Keywords:Algorithms;Greedy;Dynamic Programming;Online;Randomized;Loop InvariantReview:0

Chapter 1

Preliminaries

It is commonly believed that more than 70% (!) of the effort and cost of developing a complex software system is devoted, in one way or another, to error correcting.

Algorith., pg. 107 [Harel (1987)]

1.1What is correctness?

To show that an algorithm is correct, we must show somehow that it does what it is supposed to do. The difficulty is that the algorithm unfolds in time, and it is tricky to work with a variable number of steps, i.e., while-loops. We are going to introduce a framework for proving algorithm (and program) correctness that is called Hoare’s logic. This framework uses induction and invariance (see Section 9.1), and logic (see Section 9.4) but we are going to use it informally. For a formal example see Section 9.4.4.

We make two assertions, called the pre-condition and the post-condition; by correctness we mean that whenever the pre-condition holds before the algorithm executes, the post-condition will hold after it executes. By termination we mean that whenever the pre-condition holds, the algorithm will stop running after finitely many steps. Correctness without termination is called partial correctness, and correctness per se is partial correctness with termination. All this terminology is there to connect a given problem with some algorithm that purports to solve it. Hence we pick the pre and post condition in a way that reflects this relationship and proves it true.

These concepts can be made more precise, but we need to introduce some standard notation: Boolean connectives: ∧ is “and,” ∨ is “or” and ¬ is “not.” We also use → as Boolean implication, i.e., x → y is logically equivalent to ¬x ∨ y, and ↔ is Boolean equivalence, and α ↔ β expresses ((α → β) ∧ (β →α)). ∀ is the “for-all” universal quantifier, and ∃ is the “there exists” existential quantifier. We use “⇒” to abbreviate the word “implies,” i.e., 2|x ⇒ x is even, while “⇏” abbreviates “does not imply.”

Let A be an algorithm, and let

be the set of all well-formed inputs for A; the idea is that if I ∈

then it “makes sense” to give I as an input to A. The concept of a “well-formed” input can also be made precise, but it is enough to rely on our intuitive understanding—for example, an algorithm that takes a pair of integers as input will not be “fed” a matrix. Let O = A(I) be the output of A on I, if it exists. Let α_A be a precondition and β_A a post-condition of A; if I satisfies the pre-condition we write α_A(I) and if O satisfies the post-condition we write β_A(O). Then, partial correctness of A with respect to pre-condition α_A and post-condition β_A can be stated as:

In words: for any well formed input I, if I satisfies the pre-condition and A(I) produces an output (i.e., terminates), then this output satisfies the post-condition.

Full correctness is (1.1) together with the assertion that for all I ∈

, A(I) terminates (and hence there exists an O such that O = A(I)).

Problem 1.1. Modify (1.1) to express full correctness.

A fundamental notion in the analysis of algorithms is that of a loop invariant; it is an assertion that stays true after each execution of a “while” (or “for”) loop. Coming up with the right assertion, and proving it, is a creative endeavor. If the algorithm terminates, the loop invariant is an assertion that helps to prove the implication α_A(I) → β_A(A(I)).

Once the loop invariant has been shown to hold, it is used for proving partial correctness of the algorithm. So the criterion for selecting a loop invariant is that it helps in proving the post-condition. In general many different loop invariants (and for that matter pre and post-conditions) may yield a desirable proof of correctness; the art of the analysis of algorithms consists in selecting them judiciously. We usually need induction to prove that a chosen loop invariant holds after each iteration of a loop, and usually we also need the pre-condition as an assumption in this proof.

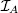
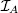
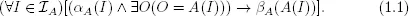
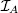
1.1.1Complexity

Given an algorithm

and an input x, the running time of

on x is the number of steps it takes

to terminate on input x. The delicate issue here is to define a “step,” but we are going to be informal about it: we assume a Random Access Machine (a machine that can access memory cells in a single step), and we assume that an assignment of the type x ← y is a single step, and so are arithmetical operations, and the testing of Boolean expressions (such as x ≥ y ∧ y ≥ 0). Of course this simplification does not reflect the true state of affairs if for example we manipulate numbers of 4,000 bits (as in the case of cryptographic algorithms). But then we redefine steps appropriately to the context.

We are interested in worst-case complexity. That...

Table of contents

• Cover Page
• Title
• Copyright
• Dedication
• Preface
• Contents
• 1. Preliminaries
• 2. Greedy Algorithms
• 3. Divide and Conquer
• 4. Dynamic Programming
• 5. Online Algorithms
• 6. Randomized Algorithms
• 7. Algorithms in Linear Algebra
• 8. Computational Foundations
• 9. Mathematical Foundations
• Bibliography
• Index