Mathematics Almost Everywhere

In Memory of Solomon Marcus

Alexandra Bellow, Cristian S Calude, Tudor Zamfirescu

• Publisher: WSPC
• Year: 2018
• eBook ISBN: 9789813237322
• Topic: Computer Science
• Subtopic: Computer Science General
• Index: Computer Science

-->

The book is a collection of original papers, research and surveys, dedicated to the memory of the Romanian mathematician Solomon Marcus (1925–2016). Marcus published many papers and books in mathematical analysis, theoretical computer science, mathematical linguistics, poetics, theory of literature, semiotics, and several other fields less strongly connected to mathematics, like cultural anthropology, biology, history and philosophy of science, education. He exemplified an unimaginable richness of ideas.

This volume intends to emphasize the mathematical fields in which Solomon Marcus worked, and demonstrate — as he also did — the interconnection between them. The authors who contribute to this volume are well-known experts in their fields. Most of them knew Solomon Marcus well, some even owed him for his decisive impulses for their careers and general development. With articles in so diverse areas, the volume will attract readers who would like to diversify their own knowledge or find unexpected connections with other topics.

-->
--> Contents:

• Logic, Complexity and Algebra:
  • On Bases of Many-Valued Truth Functions (A Salomaa)
  • Quasiperiods of Infinite Words (L Staiger)
  • Early Romanian Contributions to Algebra and Polynomials (D Ştefănescu)
  • Distributed Compression through the Lens of Algorithmic Information Theory: A Primer (M Zimand)
• Integrals, Operators, AF Algebras, Proof Mining and Monotone Nonexpansive Mappings:
  • Monotonically Controlled Integrals (T Ball, D Preiss)
  • Fine Properties of Duality Mappings (G Dincă)
  • Primitive Ideal Spaces of Postliminal AF Algebras (A Lazar)
  • An Application of Proof Miningto the Proximal Point Algorithm in CAT(0) Spaces (L Leuştean, A Sipoş)
  • Generic Well-posedness of the Fixed Point Problem for Monotone Nonexpansive Mappings (S Reich, A J Zaslavski)
• Linguistics, Computer Science and Physics:
  • Analytical Linguistics and Formal Grammars: Contributions of Solomon Marcus and Their Further Developments (M Burgin)
  • A Contagious Creativity (Gh Păun)
  • Entanglement through Path Identification (K Svozil)
• Solomon Marcus in Context:
  • Memories about Solomon Marcus (A Bruckner)
  • Memories With and About My Uncle (M Marcus)
• Index

-->
--> Readership: Graduate students and researchers. -->
Keywords:Discrete Mathematics;Mathematical Analysis;Complexity Theory;Proof Mining;Mathematical Biology;Formal Languages;Theoretical Mechanics;Mathematical Linguistics;Theoretical PhysicsReview: Key Features:

• New results in a variety of mathematical areas including operator theory, measure theory, real and functional analysis, computable algebra, formal languages, proof mining in nonlinear analysis, theoretical mechanics, mathematical logic, and topical surveys in mathematical linguistics, complexity theory and computational biology
• The authors, coming from various parts of the world, are well-known experts in the areas of their contributions
• Interconnections between results and domains will make the volume not only informative, but also attractive and unique

Chapter 1

On Bases of Many-Valued Truth Functions

Arto Salomaa

Turku Centre for Computer Science

University of Turku, Quantum 392, 20014 Turun yliopisto, Finland
[email protected]

Abstract. Truth functions in n-valued logic, n ≥ 2, can be viewed as functions from a Cartesian power of a finite set (the set of truth values) consisting of n elements into the set itself. This partly expository paper will deal with some important and formally beautiful results about the composition theory of truth functions and the resulting classes of functions. Striking differences between the cases n = 2 and n ≥ 3 are obtained.

1.1 Preliminaries

Consider functions f(x₁, . . . , x_k) of finitely many variables, ranging over a fixed finite set S with n ≥ 2 elements, and whose values are in S, that is, functions whose domain is the Cartesian power S^k and whose range is included in S. The class of such functions is denoted by

_S,

_n, or simply

if n is understood.

When we speak of functions in this paper, we always mean functions in

_S, and n refers to the cardinality card(S) of S = {1, . . . , n}.

There are nⁿ functions of one variable, whereas the total number of functions of k variables is n^nk. Although these numbers are finite, in the classes considered below the number k of variables is unbounded. A specific function can always be defined by listing the function values for different combinations of the argument values.

This set-up occurs in many diverse situations, [3]. The interpretation we have in mind in this paper is many-valued logic. The set S consists of n truth values, and the functions are truth functions. However, the material in this paper is independent of any interpretation and semantic considerations concerning the “meaning” of the truth values are irrelevant. Axiomatization of many-valued logics, [6, 8, 13], lies outside the scope of the paper.

For any subclass

of functions, we consider compositions of functions in

. For instance, starting with a binary function f(x, y), we obtain among others the following functions:

We omit here the formal definition of compositions. Compositions must be expressed in terms of function symbols, and variables coming from a denumerably infinite supply. Elements of S may not appear in compositions.

If a function is expressed as a composition of some functions, we say that the latter functions generate the former function.

Definition 1.1. The closure CL(

) of a class

of functions consists of all functions generated by functions in

. A class of functions

is closed if CL(

) =

. A subclass

₁ of a class

of functions is said to be complete in

if

Classes complete in

_n are termed, briefly, complete. A complete subclass of

is a basis of

if no proper subclass of it is complete in

.

It is well-known that, for any n, there are singleton complete classes. Functions in such single...

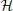
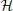
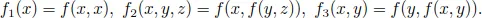
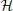
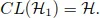
Table of contents

• Cover page
• Title page
• Copyright
• Dedication
• Preface
• Contents
• Logic, Complexity and Algebra
• 1. On Bases of Many-Valued Truth Functions
• 2. Quasiperiods of Infinite Words
• 3. Early Romanian Contributions to Algebra and Polynomials
• 4. Distributed Compression through the Lens of Algorithmic Information Theory: A Primer
• 5. Monotonically Controlled Integrals
• 6. Fine Properties of Duality Mappings
• 7. Primitive Ideal Spaces of Postliminal AF Algebras
• 8. An Application of Proof Mining to the Proximal Point Algorithm in CAT(0) Spaces
• 9. Generic Well-posedness of the Fixed Point Problem for Monotone Nonexpansive Mappings
• 10. Analytical Linguistics and Formal Grammars: Contributions of Solomon Marcus and Their Further Developments
• 11. A Contagious Creativity
• 12. Entanglement through Path Identification
• 13. Memories about Solomon Marcus
• 14. Memories With and About My Uncle
• Index