Integration for Calculus, Analysis, and Differential Equations

Techniques, Examples, and Exercises

Marat V Markin

• Publisher: WSPC
• Year: 2018
• eBook ISBN: 9789813272057
• Topic: Mathematics
• Subtopic: Calculus
• Index: Mathematics

-->

The book assists Calculus students to gain a better understanding and command of integration and its applications. It reaches to students in more advanced courses such as Multivariable Calculus, Differential Equations, and Analysis, where the ability to effectively integrate is essential for their success.

Keeping the reader constantly focused on the three principal epistemological questions: " What for? ", " Why? ", and " How? ", the book is designated as a supplementary instructional tool and consists of

-->

• 9 Chapters treating the three kinds of integral: indefinite, definite, and improper. Also covering various aspects of integral calculus from abstract definitions and theorems (with complete proof whenever appropriate) through various integration techniques to applications,
• 3 Appendices containing a table of basic integrals, reduction formulas, and basic identities of algebra and trigonometry.

It also contains

• 143 Examples, including 112 thoughtfully selected Problems with complete step-by-step solutions, the same problem occasionally solved in more than one way while encouraging the reader to find the most efficient integration path, and
• 6 Exercises, 162 Practice Problems offered at the end of each chapter starting with Chapter 2 as well as 30 Mixed Integration Problems "for dessert", where the reader is expected to independently choose and implement the best possible integration approach.

-->

The Answers to all the 192 Problems are provided in the Answer Key. The book will benefit undergraduates, advanced undergraduates, and members of the public with an interest in science and technology, helping them to master techniques of integration at the level expected in a calculus course.

--> Sample Chapter(s)
Chapter 1: Indefinite and Definite Integrals

Request Inspection Copy

--> Contents:

• Preface
• Indefinite and Definite Integrals
• Direct Integration
• Method of Substitution
• Method of Integration by Parts
• Trigonometric Integrals
• Trigonometric Substitutions
• Integration of Rational Functions
• Rationalizing Substitutions
• Can We Integrate Them All Now?
• Improper Integrals
• Mixed Integration Problems
• Answer Key
• Appendices:
  • Table of Basic Integrals
  • Reduction Formulas
  • Basic Identities of Algebra and Trigonometry
• Bibliography
• Index

--> -->
Readership: Undergraduates, advanced undergraduates and members of the public with an interest in integration and its applications. -->Indefinite Integral;Definite Integral;Improper Integral;Direct Integration;Method of Substitution;Integration by Parts0 Key Features:

• The book contains a wealth of examples and thoughtfully selected problems with complete step-by-step solutions, while providing several methods of solving the same problem
• A chapter dedicated to direct integration, i.e. integration, which, using the integration rules alone, reduces the integral of a given function to a combination of table integrals and making no use of any special integration techniques

Chapter 1

Indefinite and Definite Integrals

1.1.Antiderivatives and Indefinite Integral

1.1.1.Definitions and Examples

Definition 1.1 (Antiderivative).

Let f be a function defined on an interval I. A function F is called an antiderivative of f(x) on I if

Examples 1.1 (Antiderivatives).

1.The function F(x) = 1 is an antiderivative of f(x) = 0 on (–∞, ∞) as well as any function of the form F(x) = C, where C is an arbitrary real constant (written henceforth as C

R).

2.The function F(x) = x is an antiderivative of f(x) = 1 on (–∞, ∞) as well as any function of the form F(x) = x + C, C

R.

3.The function

is an antiderivative of f(x) = x on (–∞, ∞) as well as any function of the form

.

4.Any function of the form F(x) = e^x + C, C

R, is an antiderivative of f(x) = e^x on (–∞, ∞).

All the above examples have one thing in common: if F is an antiderivative of f on I, then so is any function of the form

where C is an arbitrary real constant (C

R).

The natural question is: are there antiderivatives of f on I not included in this description? The answer is NO.

As follows from the Mean Value Theorem (see, e.g., [1, 6]), functions with the same derivative differ by a constant. Thus, if G is an arbitrary antiderivative of f on I, there is a C

R such that

and hence, expression (1.1) describes all possible antiderivatives of f on I.

Definition 1.2 (Indefinite Integral).

Let a function f defined on an interval I have an antiderivative F on I. The indefinite integral (or the general antiderivative) of f on I is the expression

where C is an arbitrary real constant (C

R).

The integral notation

...

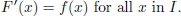
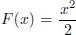
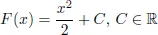
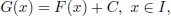
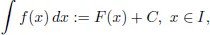
Table of contents

• Cover
• Halftitle
• Title
• Copyright
• Dedication
• Contents
• Preface
• 1. Indefinite and Definite Integrals
• 2. Direct Integration
• 3. Method of Substitution
• 4. Method of Integration by Parts
• 5. Trigonometric Integrals
• 6. Trigonometric Substitutions
• 7. Integration of Rational Functions
• 8. Rationalizing Substitutions
• Can We Integrate Them All Now?
• 9. Improper Integrals
• Mixed Integration Problems
• Answer Key
• Appendix A Table of Basic Integrals
• Appendix B Reduction Formulas
• Appendix C Basic Identities of Algebra and Trigonometry
• Bibliography
• Index