Molecular Vibrations

An Algebraic and Nonlinear Approach

Guozhen Wu

• Publisher: WSPC
• Year: 2018
• eBook ISBN: 9789813270718
• Topic: Physical Sciences
• Subtopic: Atomic & Molecular Physics

-->

This book focuses on the main idea that highly-excited molecular vibration is a nonlinear, many-body and semiclassical system. Therefore, many ideas and techniques in nonlinear fields such as chaos, resonance, Lyapunov exponent, etc. can be incorporated into this study. Together with the Lie algebraic coset algorithm, readers are able to approach the topics in a simple arithmetic and realistic way in contrast to the traditional solving of Schrödinger equation.

Covering the author's research in over two decades, these works bridge the gaps between molecular vibration and nonlinear sciences, many new characters are introduced for molecular highly-excited vibration from a fresh viewpoint of nonlinearity, especially, the chaos. Related works of the elementary ideas in this field can be found in the first three chapters for the readers to be familiar with, while the rest of the chapters offer concrete examples with flourishing ideas and results on system dynamics which are not known or neglected by the traditional wave function algorithm.

--> Sample Chapter(s)
1. Pendulum Dynamics --> Contents:

• Preface
• Pendulum Dynamics
• Algebraic Approach to Vibrational Dynamics
• Chaos
• C–H Bending Motion of Acetylene
• Assignments and Classification of Vibrational Manifolds
• Dixon Dip
• Quantization by Lyapunov Exponent and Periodic Trajectories
• Dynamics of DCO/HCO and Dynamical Barrier Due to Extremely Irrational Couplings
• Dynamical Potential Analysis for HCP, DCP, N 2 O, HOCl and HOBr
• Chaos in the Transition State Induced by the Bending Motion

--> -->
Readership: Postgrads and researchers in nonlinear science and analysis.
-->Nonlinear Science;Molecular Vibration;Algebraic Method;Nonlinear Method;Chaos0 Key Features:

• It broadens the prospects of molecular vibration to high excitation
• It broadens the treatment of molecular vibration to algebraic and nonlinear methods

Chapter 1

Pendulum Dynamics

1.1Pendulum dynamics

The motion of a pendulum is well known. We will demonstrate throughout in this monograph that in fact, it plays an essential role in dynamics.

Shown in Fig. 1.1 is the configuration of a pendulum with coordinate, θ and its potential, V which is proportional to 1 − cos θ. As θ = 0, its potential is minimal. As θ = π, it reaches the highest point and its potential is maximal. If its kinetic energy is not large enough, the pendulum will be bound in the region between −π and π and its motion is periodic. In this situation, if the energy is small enough, that 1 − cos θ = 2sin² θ/2 can be approximated by θ²/2 (via sin θ ≈ θ), then the motion is the simple harmonic oscillator and the period is a constant, independent of the motion amplitude. Of course, for the motion with larger amplitude, the period will be energy dependent and the motion is called nonlinear or anharmonic. Since the potential valley is wider at its top, if the energy is quantized, the nearest neighboring level spacing will be smaller near the valley top. This is shown also in Fig. 1.1. As the pendulum energy is larger than the potential at θ = π, the pendulum will rotate clockwise or counter-clockwise so the angle may be extended indefinitely. The clockwise and counter-clockwise rotations are equivalent with opposite actions. Shown in Fig. 1.2 is its phase diagram where J is the rotational action (angular momentum). Figure 1.2 depicts the pendulum dynamics in a succinct way in which the periodic motions are the circles and the freely rotating motions are the up-and-down curves. The periodic motion is bound in a limited region while the rotating motion is unbound. These two motions are of different characters dynamically. They are separated by the curve labelled by S, called the separatrix. Besides, the two fixed points, a and b, deserve attention. Point a is dynamically stable while b is unstable where the pendulum is at its highest position. It deserves to note that point b is just the cross point of the two separatrix lines where the line (or flow line) directions are opposite: one is toward while the other is away from point b, just like that of a saddle (hyperbola). Hence, this unstable fixed point is also called the saddle point where along one direction, the dynamics is stable while along the other unstable. We will see that in higher dimensions, the region near the saddle point is where chaotic motion will emerge first if it occurs. This was first visualized by Poincare who pointed out that once the stable and unstable orbits originating from the same saddle point intersect once, then they will intersect infinite times, forming the so-called homoclinic tangle. Thus, chaos forms around the saddle fixed point. The tangling orbit will approach the fixed point in an exponentially decelerating way and will never reach the fixed point.

Fig. 1.1 The configuration of a pendulum with coordinate, θ and its potential, V which is proportional to 1 − cos θ. The horizontal lines in the potential valley show the quantized levels. Due to the nonlinear effect, the nearest neighboring level spacing is less for higher levels.

Fig. 1.2 The phase diagram of the motion of a pendulum. J is the action and θ is the angle. Curves correspond to the various quantized levels. Arrows denote the directions of motion. A, A′ show the opposite rotations. S is the separatrix. a and b are the stable and unstable fixed points, respectively.

This is a very important milestone as far as the developing of the chaotic dynamics is concerned. It deserves to quote what Poincare wrote in his New Methods of Celestial Mechanics in 1899: When we try to represent the figures formed by these two curves and their infinitely many intersections, . . . these intersections form a type of trellis, tissue or grid with infinitely fine mesh; neither of the two curves must ever cut across itself again, but it must bend back upon itself in a very complex manner in order to cut across all of the meshes in the grid an infinite number of times. The complexity of this figure is striking, and I shall not even try to draw it. Nothing is more suitable for providing us with an idea of the complex nature of the three body problem and of all the problems of dynamics in general. Poincare found this phenomenon in his study of the three body problem. He also visualized that this chaotic issue is quite general.

We summarize the dynamical ideas embedded in the pendulum motion: (1) The harmonic and anharmonic periodic motions. The motion period of the former is energy (or action) independent while the latter is energy dependent. This difference can be used to define linearity and nonlinearity for a dynamical system. (2) The separatr...

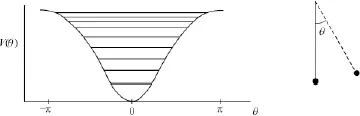
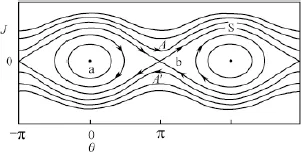
Table of contents

• Cover
• Halftitle
• Title
• Copyright
• Contents
• Preface
• 1 Pendulum Dynamics
• 2 Algebraic Approach to Vibrational Dynamics
• 3 Chaos
• 4 C–H Bending Motion of Acetylene
• 5 Assignments and Classification of Vibrational Manifolds
• 6 Dixon Dip
• 7 Quantization by Lyapunov Exponent and Periodic Trajectories
• 8 Dynamics of DCO/HCO and Dynamical Barrier Due to Extremely Irrational Couplings
• 9 Dynamical Potential Analysis for HCP, DCP, N2O, HOCl and HOBr
• 10 Chaos in the Transition State Induced by the Bending Motion
• Appendix: Author’s Publications Related to this Monograph