The Imperial College Lectures in Petroleum Engineering

Volume 5: Fluid Flow in Porous Media

Robert W Zimmerman

• Publisher: WSPC (EUROPE)
• Year: 2018
• eBook ISBN:
  9781786345011
• Topic: Tecnología e ingeniería
• Subtopic: Ingeniería química y bioquímica

This book presents, in a self-contained form, the equations of fluid flow in porous media, with a focus on topics and issues that are relevant to petroleum reservoir engineering. No prior knowledge of the field is assumed on the part of the reader, and particular care is given to careful mathematical and conceptual development of the governing equations, and solutions for important reservoir flow problems. Fluid Flow in Porous Media starts with a discussion of permeability and Darcy's law, then moves on to a careful derivation of the pressure diffusion equation. Solutions are developed and discussed for flow to a vertical well in an infinite reservoir, in reservoirs containing faults, in bounded reservoirs, and to hydraulically fractured wells. Special topics such as the dual-porosity model for fractured reservoirs, and fluid flow in gas reservoirs, are also covered. The book includes twenty problems, along with detailed solutions.

As part of the Imperial College Lectures in Petroleum Engineering, and based on a lecture series on the same topic, this book provides the introductory information needed for students of the petroleum engineering and hydrology.

Contents:

• Pressure Diffusion Equation for Fluid Flow in Porous Rocks
• Line Source Solution for a Vertical Well in an Infinite Reservoir
• Superposition and Pressure Buildup Tests
• Effect of Faults and Linear Boundaries
• Wellbore Skin and Wellbore Storage
• Production From Bounded Reservoirs
• Laplace Transform Methods in Reservoir Engineering
• Naturally-Fractured Reservoirs
• Flow of Gases in Porous Media
• Appendix: Solutions to Problems
• Nomenclature List
• References
• Index

Readership: Undergraduate and postgraduate students of petroleum engineering or hydrology.

Chapter 1

Pressure Diffusion Equation for Fluid Flow in Porous Rocks

In this chapter, we will derive the basic differential equations that govern the time-dependent flow of fluids through porous media such as rocks or soils. This will be done by combining the principle of conservation of mass with Darcy’s law, which relates the flow rate to the pressure gradient. The resulting differential equation will be a diffusion-type equation that governs the way that the fluid pressure changes as a function of time and varies spatially throughout the reservoir. The governing equations derived in this chapter form the basis of analytical models that are used in well test analysis, and, in discretised form, form the basis of numerical simulation codes that are used in petroleum reservoir engineering to predict oil and gas recovery.

1.1. Darcy’s Law and the Definition of Permeability

The basic law governing the flow of fluids through porous media is Darcy’s law, which was formulated by the French civil engineer Henry Darcy in 1856 on the basis of his experiments on vertical water filtration through sand beds. Darcy (1856) found that his data could be described by

where P is the pressure (Pa), ρ is the density (kg/m³), g is the gravitational acceleration (m/s²), z is the vertical coordinate (measured downwards) (m), L is the length of sample (m), Q is the volumetric flow rate (m³/s), C is the constant of proportionality (m²/Pa s), and A is the cross-sectional area of the sample (m²).

Any consistent set of units can be used in Darcy’s law, such as SI units, cgs units, British engineering units, etc. Unfortunately, in the oil and gas industry it is common to use so-called “oilfield units”, which are not self-consistent. Oilfield units (i.e. barrels, feet, pounds per square inch, etc.) will not be used in these notes, except occasionally in some of the problems.

Darcy’s law is mathematically analogous to other linear phenomenological transport laws, such as Ohm’s law for electrical conduction, Fick’s law for solute diffusion, and Fourier’s law for heat conduction.

Why does the term “P − ρgz” govern the flow rate? Recall from elementary fluid mechanics that Bernoulli’s equation, which essentially embodies the principle of “conservation of energy”, contains the terms

where P/ρ is related to the enthalpy per unit mass, −gz is the gravitational energy per unit mass, and v²/g is the kinetic energy per unit mass. Fluid velocities in a reservoir are usually very small, and so the third term is usually negligible, in which case we see that the combination P − ρgz represents an energy-type term. It seems reasonable that fluid would flow from regions of higher energy to lower energy, and, therefore, the driving force for flow should be the gradient (i.e. the rate of spatial change) of P −ρgz.

Subsequent to Darcy’s initial discovery, it has been found that, all other factors being equal, Q is inversely proportional to the fluid viscosity, μ (Pa s). It is therefore convenient to factor out μ, and put C = k/μ, where k is known as the permeability, with dimensions (m²).

It is usually more convenient to work with the volumetric flow per unit area, q = Q/A, rather than the total flow rate, Q. In terms of q, Darcy’s law can be written as

where the flux q has dimensions of (m/s). Since q is not quite the same as the velocity of the individual fluid particles (see Eq. (9.4.5)), it is perhaps better to think of these units as (m³/m²s).

For transient processes in which the flux varies from point-to-point in a reservoir, we need a differential form of Darcy’s law. In the vertical direction, this equation takes the form

where z is the downward-pointing vertical coordinate. The minus sign is included because the fluid flows in the direction from higher to lower values of P −ρgz.

Since z is constant in the horizontal direction, the differential form of Darcy’s law for one-dimensional (1D) horizontal flow is

For most sedimentary rocks, the permeability in the horizontal plane, k_H, is different than permeability in the vertical direction, k_V. Typically, k_H > k_V. The permeabilities in any two orthogonal directions within the horizontal plane may also differ. However, in these notes we will usually assume that k_H = k_V, and denote the permeability by k.

The permeability is a function of rock type, and also varies with stress, temperature, etc., but does not depend on the fluid; the effect of the fluid on the flow rate is accounted for by the viscosity term in Eq. (1.1.4) or (1.1.5).

Permeability has units of m², but in the petroleum industry it is conventional to use “Darcy” units, defined by

The Darcy unit is defined such that a rock having a permeability of 1 Darcy would transmit 1 cm³ of water (wh...

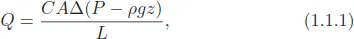
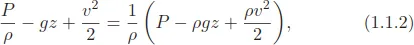
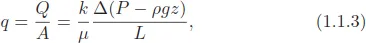
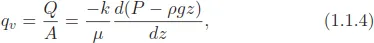
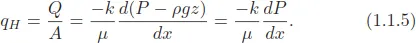
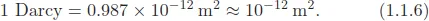
Table of contents

• Cover page
• Title
• Copyright
• Preface
• About the Author
• Chapter 1. Pressure Diffusion Equation for Fluid Flow in Porous Rocks
• Chapter 2. Line Source Solution for a Vertical Well in an Infinite Reservoir
• Chapter 3. Superposition and Pressure Buildup Tests
• Chapter 4. Effect of Faults and Linear Boundaries
• Chapter 5. Wellbore Skin and Wellbore Storage
• Chapter 6. Production From Bounded Reservoirs
• Chapter 7. Laplace Transform Methods in Reservoir Engineering
• Chapter 8. Naturally-Fractured Reservoirs
• Chapter 9. Flow of Gases in Porous Media
• Appendix: Solutions to Problems
• Nomenclature
• References
• Index