A Guide to Mathematical Methods for Physicists

Advanced Topics and Applications

Michela Petrini, Gianfranco Pradisi;Alberto Zaffaroni

• Publisher: WSPC (EUROPE)
• Year: 2018
• eBook ISBN: 9781786345509
• Topic: Physical Sciences
• Subtopic: Mathematical & Computational Physics

This book provides a self-contained and rigorous presentation of the main mathematical tools needed to approach many courses at the last year of undergraduate in Physics and MSc programs, from Electromagnetism to Quantum Mechanics. It complements A Guide to Mathematical Methods for Physicists with advanced topics and physical applications. The different arguments are organised in three main sections: Complex Analysis, Differential Equations and Hilbert Spaces, covering most of the standard mathematical method tools in modern physics.

One of the purposes of the book is to show how seemingly different mathematical tools like, for instance, Fourier transforms, eigenvalue problems, special functions and so on, are all deeply interconnected. It contains a large number of examples, problems and detailed solutions, emphasising the main purpose of relating concrete physical examples with more formal mathematical aspects.

Contents:

• Complex Analysis:
  • Introduction
  • Mapping Properties of Holomorphic Functions
  • Laplace Transform
  • Asymptotic Expansions
• Differential Equations:
  • Introduction
  • The Cauchy Problem for Differential Equations
  • Boundary Value Problems
  • Green Functions
  • Power Series Methods
• Hilbert Spaces:
  • Introduction
  • Compact Operators and Integral Equations
  • Hilbert Spaces and Quantum Mechanics
• Appendices:
  • Review of Basic Concepts
  • Solutions of the Exercises

Readership: Students and professionals in the field.
Mathematical Methods0 Key Features:

• This book treats the chosen topics in depth, always keeping in mind physical applications and practical aspects
• The book contains many examples and exercises with solutions. This is of course of practical use for the students, and it is also meant to stress the main purpose of relating concrete physical examples with more formal mathematical aspects

PART I

Complex Analysis

Introduction

Complex analysis is very rich and interesting. A central role is played by holomorphic functions. These are functions of a complex variable, f :

→

, that are differentiable in complex sense. Differentiability on C is stronger than in the real sense and has important consequences for the behaviour of holomorphic functions. For instance, holomorphic functions are infinitely differentiable and analytic, and do not admit local extrema. The basic properties of holomorphic functions are discussed in the first volume of this book (see Petrini et al., 2017) and are briefly summarised in Appendix A. In this volume we will discuss some extensions and applications of complex analysis that are relevant for physics. Typical applications are conformal mapping, integral transforms and saddle-point methods.

The idea of conformal mapping is to consider holomorphic functions as maps from the complex plane to itself. As holomorphic functions are analytic, these maps have very specific features. For instance, a bijective holomorphic function f preserves angles, namely it maps two lines intersecting in a point z₀ with a given angle to two curves whose tangents intersect in f(z₀) with the same angle. Such a map f is called conformal. Conformal transformations can be used to map domains of the complex plane to simpler ones. In particular, any domain Ω ⊂

can be mapped to the unit disk by an appropriately chosen conformal map. This is very useful in physics to solve problems in two dimensions. As we will see in Section 1.3, one can find solutions of the Laplace equation on complicated domains of the plane by mapping them to the corresponding solution on the unit disk.

A tool to solve differential equations is provided by integral transforms. An example is the Laplace transform

where f is a function of one real variable and s is a complex number. The Laplace transform can be seen as a holomorphic generalisation of the Fourier transform¹ and, as we will see, is very useful to solve Cauchy problems for linear differential equations (see Chapter 4), namely finding a solution of a differential equation that also satisfies given initial conditions.

Another useful application of complex analysis is given by the saddle-point method, which allows to estimate the behaviour of integrals of the type

with γ a curve on the complex plane and h(z) and g(z) holomorphic functions, for large values of the real parameter x. A similar analysis can be also performed for integrals of Laplace type or generalisations thereof. This is the realm of asymptotic analysis, which we discuss in Chapter 3. As we will see in Chapter 7, asymptotic expansions can also be applied to the study of the local behaviour of the solutions of differential equations. Linear differential equations with non-constant coefficients can have singular points and it is interesting to see how the solutions behave in a neighbourhood of a given poin...

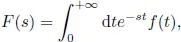
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Preface
• Contents
• Part I. Complex Analysis
• Part II. Differential Equations
• Part III. Hilbert Spaces
• Part IV. Appendices
• Bibliography
• Index