A Mathematical Modeling Approach to Infectious Diseases

Cross Diffusion PDE Models for Epidemiology

William E Schiesser

• Publisher: WSPC
• Year: 2018
• ISBN:
  9789813238800
• Topic: Tecnología e ingeniería
• Subtopic: Ciencias biomédicas

The intent of this book is to provide a methodology for the analysis of infectious diseases by computer-based mathematical models. The approach is based on ordinary differential equations (ODEs) that provide time variation of the model dependent variables and partial differential equations (PDEs) that provide time and spatial (spatiotemporal) variations of the model dependent variables.

The starting point is a basic ODE SIR (Susceptible Infected Recovered) model that defines the S,I,R populations as a function of time. The ODE SIR model is then extended to PDEs that demonstrate the spatiotemporal evolution of the S,I,R populations. A unique feature of the PDE model is the use of cross diffusion between populations, a nonlinear effect that is readily accommodated numerically. A second feature is the use of radial coordinates to represent the geographical distribution of the model populations.

The numerical methods for the computer implementation of ODE/PDE models for infectious diseases are illustrated with documented R routines for particular applications, including models for malaria and the Zika virus. The R routines are available from a download so that the reader can reproduce the reported solutions, then extend the applications through computer experimentation, including the addition of postulated effects and associated equations, and the implementation of alternative models of interest.

The ODE/PDE methodology is open ended and facilitates the development of computer-based models which hopefully can elucidate the causes/conditions of infectious disease evolution and suggest methods of control.

Contents:

• Introduction to Spatiotemporal Models
• SIR Models
• Cross Diffusion
• Alternative Coordinate Systems
• Vector-Borne Diseases, Malaria
• Vector-Borne Diseases, Zika Virus

Readership: Medical researchers, biologists, applied mathematicians, NIH, WHO, pharmaceutical companies.
Key Features:

• Partial differential equation analysis defining the spatiotemporal evolution of epidemics
• Cross diffusion between affected populations
• Radial spatial coordinates corresponding to the physical system geometry
• This combination of features does not appear in any other book of which the author is aware

Chapter 1

Introduction to Spatiotemporal Models

(1.1)Introduction

The threat of infectious diseases continues as an urgent, worldwide health problem. The monitoring and treatment of infectious diseases on large spatial scales, e.g., epidemics in geographical regions, is therefore an on-going requirement.

To better understand this requirement, particularly the evolution of epidemics in space and time, mathematical models based on partial differential equations (PDEs) are the logical choice for quantitative analysis¹

Several SIR PDE-based models have been reported in the literature. Generally the equations are sufficiently complicated that the solution of the PDEs requires a computer implementation. The PDEs are coded (programmed) to execute within an established scientific computing system (termed a language). Several languages are available. Here we select R, an open-source (no cost), quality scientific computing system that can be easily downloaded from the Internet².

Of the various PDE-SIR models that have been reported, a class of models is considered here which includes interactions with infected populations that are nonlinear³, e.g., [1]. These interaction terms represent cross diffusion. This book focuses on cross diffusion PDE-based SIR models.

The presentation is in terms of example applications, presented at an introductory level⁴. Formal mathematics, e.g., theorems and proofs, is largely avoided. The model output is displayed in terms of numerical solutions presented in graphical format (2D, 3D plots) produced by the R graphics utilities.

We next consider a series of PDE-based models in order of increasing details. R coding for these models is presented as a series of routines with output presented for each model.

(1.2)A Basic PDE Model

To start, a PDE model is derived for two components, S(x, t) (susceptibles) and I(x, t) (infecteds). x is the first dimenion in the three dimensional Cartesian coordinate system (x, y, z). t is time.

A statement of a dynamic conservation principle is the starting point for the development of the model. A population balance for S(x, t) on an incremental area LΔx gives

where (in SI (MKS) units)

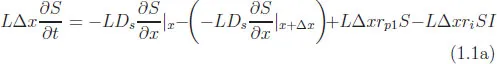
S(x, t)	S population density (susceptibles/m^2)
I(x, t)	I population density (infecteds/m^2)
x	distance (m)
t	time (s = seconds)
L	cross sectional length of incremental area (m)
Ds	effective diffusivity for the susceptibles (m^2/s)
rp1	net S population growth rate (birth rate - death rate) (1/s)
ri	grow rate from S and I interactions ((m^2/infecteds) (1/s))

Eq. (1.1a) is based on partial derivatives, e.g.,

, since the dependent variable S(x, t) is a function of two independent variables, (x, t). Therefore, the independent variable must be identified in each of the derivatives (derivatives with respect to x and t appear in the following discussion).

The terms in eq. (1.1a) have the following interpretation:

•

: Accumulation (if > 0 or depletion if < 0)) of susceptibles in the incremental area LΔx with units: (m)(m)(susceptibles/m²)(1/s)=susceptibles/s

•

: Effective diffusion of susceptibles into the incremental area at x, with units: (m)(m²/s)(susceptibles/m²)(1/m) = susceptibles/s. This term is based on the assumption that the spatial movement of the susceptibles is modeled as 1D diffusion which represents random motion. If the movement is more directed, this term can be supplemented by convection (a directed flow).

The net flux (random movement per unit length), q_x, is given by

Eq. (1.1b) is generally termed Fick’s first law. The minus is included so that the flux is in the positive x direction when the gradient

, that is, the flux i...

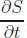
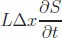
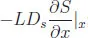
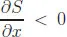
Table of contents

• Cover Page
• Title
• Copyright
• Dedication
• Contents
• Preface
• Chapter 1. Introduction to Spatiotemporal Models
• Chapter 2. SIR Models
• Chapter 3. Cross Diffusion
• Chapter 4. Alternative Coordinate Systems
• Chapter 5. Vector-Borne Diseases, Malaria
• Chapter 6. Vector-Borne Diseases, Zika Virus
• Appendix A1: Function dss004
• Appendix A2: Function dss044
• Index