Ordinary Differential Equations and Boundary Value Problems

Volume II: Boundary Value Problems

John R Graef, Johnny Henderson;Lingju Kong;Xueyan Sherry Liu

• Publisher: WSPC
• Year: 2018
• eBook ISBN: 9789813274044
• Topic: Mathematics
• Subtopic: Differential Equations
• Index: Mathematics

The authors give a systematic introduction to boundary value problems (BVPs) for ordinary differential equations. The book is a graduate level text and good to use for individual study. With the relaxed style of writing, the reader will find it to be an enticing invitation to join this important area of mathematical research. Starting with the basics of boundary value problems for ordinary differential equations, linear equations and the construction of Green's functions are presented clearly.

A discussion of the important question of the existence of solutions to both linear and nonlinear problems plays a central role in this volume and this includes solution matching and the comparison of eigenvalues.

The important and very active research area on existence and multiplicity of positive solutions is treated in detail. The last chapter is devoted to nodal solutions for BVPs with separated boundary conditions as well as for non-local problems.

While this Volume II complements Volume I: Advanced Ordinary Differential Equations, it can be used as a stand-alone work.

Contents:

• Introduction to Boundary Value Problems
• Linear Problems and Green's Functions
• Existence of Solutions I
• Existence of Solutions II
• Solution Matching
• Comparison of Smallest Eigenvalues
• BVP's for Functional Differential Equations
• Positive Solutions
• Boundary Data Smoothness
• Nodal Solutions of BVP's fpr PDE's

Readership: Undergraduate and graduate students as well as researchers who are interested in ordinary differential equations.
Key Features:

• This book is unique in that the title is descriptive of its contents, it addresses a range of questions that are timely and provides avenues for additional research, and the exercises and examples nicely illustrate the theory
• There are literally hundreds of researchers who work in the field of boundary value problems for ordinary differential equations, for functional differential equations, and for finite difference equations. This book touches each of those topics, in more depth for some, and only on the surface for others
• BVPs for functional differential equations are discussed in a separate chapter that can be omitted in a first reading

Chapter 1

Introduction to Boundary Value Problems

1.1Introduction

A boundary value problem (BVP) for an ordinary differential equation (ODE) will consist of an ODE together with conditions specified at more than one point. In particular, we will be concerned with solving scalar differential equations, y⁽ⁿ⁾ = f(x, y, y′, …, y⁽ⁿ⁻¹⁾), n ≥ 2, where f is real-valued and boundary conditions (BC’s) on solutions of the equation are specified at k, (with k ≥ 2), points belonging to some interval of the reals. Let us first consider some difficulties which might occur.

Example 1.1. Linear equations (Initial Value Problems (IVP’s) have unique solutions which extend to maximal intervals of existence).

Consider y′′ + y = 0, y(0) = 0, y(π) = 1. The general solution is y = c₁ cos x+c₂ sin x and it exists on

. Also, from the boundary conditions, we have 0 = y(0) = c₁ but y(π) = 0 ≠ 1. So, the BVP has no solution.

Exercise 1. If equations are not linear, solutions may not extend to an interval.

Consider y′′ = 1 + (y′)². Solve this equation. Show that if x₂ − x₁ ≥ π, then no solution starting at x₁, (i.e., y(x₁) = y₁), ever reaches x₂. (i.e., we cannot have a BVP with y(x₁) = y₁ and y(x₂) = y₂, whenever x₂ − x₁ ≥ π).

Example 1.2. Another question involves uniqueness of solutions of BVP’s when solutions exist.

Consider y′′ = 0, y′(0) = 0, y′(1) = 0. Then y(x) ≡ k, where k is a constant, constitutes infinitely many solutions.

Thus, questions we will be concerned with center around the existence and uniqueness of solutions of BVP’s for ODE’s. We will first consider such questions for BVP’s of linear differential equations. In this case, let L : C⁽ⁿ⁾(I) → C(I) be the linear differential operator given by

where the a_i, i = 0, 1, …, n − 1, are continuous on the interval I. Also consider the differential equation:

where f(x) is continuous on the interval I. IVP’s for (1.1) are uniquely solvable on I and all solutions of (1.1) extend to I.

Let us first examine the setting where f(x) ≡ 0:

and let us deal primarily with conjugate type boundary conditions.

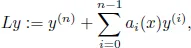
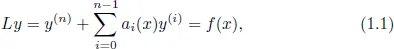
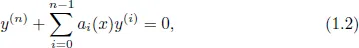
1.2Disconjugacy

Consider the third order differential equation y‴ = 0 and the BC’s, y(a) = y(b) = y(c) = 0, where a, b, c are distinct. It follows that y ≡ 0 on all of

.

Exercise 2. Show that each of the BVP’s

has only the trivial solution, where a ≠ b.

It follow...

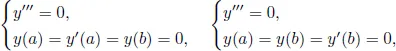
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Dedication
• Preface
• Contents
• 1. Introduction to Boundary Value Problems
• 2. Linear Problems and Green’s Functions
• 3. Existence of Solutions I
• 4. Existence of Solutions II
• 5. Solution Matching
• 6. Comparison of Smallest Eigenvalues
• 7. BVP’s for Functional Differential Equations
• 8. Positive Solutions
• 9. Boundary Data Smoothness
• 10. Nodal Solutions of BVP’s for ODE’s
• Index