`Comprises a very helpful resource for students who are obliged to succeed in passing the QTS numeracy test in order to gain QTS. It should provide a valuable resource for students to increase their confidence as well as their competence? - Mathematics in Schools
`The stated aim of this book is to help teacher-trainees prepare for the numeracy test all new entrants to the profession now have to pass. Any trainee worried about the test should find this a useful resource…. As in similar books by Derek Haylock, the mathematical content is written in a clear and accessible style? - Mike Askew, Times Educational Supplement
Quotes from the author?s students
`The book is excellent. I think it will present students and others with a valuable resource, not only to help with the QTS test, but also for teaching. I could see myself using it on "dip-in-as-necessary" basis?.
`The practice questions were really helpful for checking and consolidating learning. The material was useful for the QTS test, particularly the mental calculations. Many thanks for letting me work through your sample material. I cannot begin to tell you how much more I have learnt! This has definitely made me feel more confident about passing the QTS numeracy skills test! I have definitely demonstrated to myself from this material that my ability to complete calculations mentally has increased. I can calculate faster and with some accuracy now!?
`Comprises a very helpful resource for students who are obliged to succeed in passing the QTS numeracy test in order to gain QTS. It should provide a valuable resource for students to increase their confidence as well as their competence? - Mathemtics in Schools
This book is designed to help teacher-trainees prepare for the Qualified Teaching Standards numeracy test that must now be passed by all entrants to the teaching profession. The author focuses especially on weaknesses in numeracy often observed in adults, and in teacher-trainees in particular. As far as possible, this mathematics is set in the professional context of teaching, drawing on statistics and other data from individual schools, the DfEE and the Qualifications and Curriculum Agency (QCA).
Frequently asked questions
Yes, you can cancel anytime from the Subscription tab in your account settings on the Perlego website. Your subscription will stay active until the end of your current billing period. Learn how to cancel your subscription.
At the moment all of our mobile-responsive ePub books are available to download via the app. Most of our PDFs are also available to download and we're working on making the final remaining ones downloadable now. Learn more here.
Perlego offers two plans: Essential and Complete
Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Both plans are available with monthly, semester, or annual billing cycles.
We are an online textbook subscription service, where you can get access to an entire online library for less than the price of a single book per month. With over 1 million books across 1000+ topics, we’ve got you covered! Learn more here.
Look out for the read-aloud symbol on your next book to see if you can listen to it. The read-aloud tool reads text aloud for you, highlighting the text as it is being read. You can pause it, speed it up and slow it down. Learn more here.
Yes! You can use the Perlego app on both iOS or Android devices to read anytime, anywhere — even offline. Perfect for commutes or when you’re on the go. Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Yes, you can access Numeracy for Teaching by Derek Haylock in PDF and/or ePUB format, as well as other popular books in Education & Education General. We have over one million books available in our catalogue for you to explore.
Mental calculations, changing proportions to percentages
Without using a calculator, rewrite these statements using percentages:
a)
A quarter of the pupils in my class have free school meals.
b)
Three-quarters of the pupils in my class do not have free school meals.
c)
Seven out of eight pupils in primary schools like their teacher.
d)
This year our school had to employ a supply teacher 17 days out of 20.
e)
Four-fifths of the lessons observed by Ofsted in our school were good or very good.
f)
A total of 273 pupils out of 300 achieved at least one GCSE at grade C or above.
Answers to check-up 1
a) 25% of the pupils…
b) 75% of the pupils…
c) 87.5% of primary pupils…
d) 85% of the days…
e) 80% of the lessons…
f) 91% of the pupils…
Discussion and explanation of check-up 1
Per cent (%) means ‘for each hundred’. For example, 27% (27 per cent) means ‘27 in each hundred’, or ‘27 out of a hundred’. Percentages are useful because they give us a standard way of expressing proportions. This makes it easy to compare different proportions of pupils with free school meals in two schools if they are expressed as percentages (e.g. 37% and 35%). It is not so easy if all you have is the raw data (e.g. 170 out of 459 in one school and 238 out of 680 in the other).
Many simple proportions or fractions can be easily expressed as percentages, using mainly mental calculations. For example, the fraction one-half (
) might represent the proportion of a set of secondary pupils who own a mobile telephone. Without knowing how many pupils there are in the set, we can still express this proportion as an equivalent percentage. One-half as a proportion means ‘one out of every two pupils owns a mobile’. That’s equivalent to ‘fifty out of a hundred’, or 50%. Knowing this we can easily deduce percentage equivalents for some other common fractions. Since a quarter (
) is ‘half of a half’, then it must be equivalent to half of 50%, that is 25%. And three-quarters (
) will be three times this, which is 75%.
Eighths are a bit trickier. One-eighth is ‘half of a quarter’, so expressed as a percentage it must be ‘half of 25%’, which gives 12.5%. Knowing this, you can then work out percentage equivalents for
Actually, in example (c) I found it easier to think ‘one-eighth of the pupils do not like their teacher’, which is 12.5%, and then to subtract this from 100% to find the percentage who do like their teachers. This works because 100% represents the whole set of pupils, that is ‘100 out of 100’.
In example (d) the ‘17 out of 20’ is easily converted to an equivalent proportion out of a hundred, just by multiplying by 5. This gives ‘85 out of 100’, which is 85%.
In example (e) we can think of
as ‘4 out of 5’, which is equivalent to 80 out of 100, or 80%.
In example (f) we simply divide 273 by 3, to deduce that ‘273 out of 300’ is equivalent to ‘91 out of 100’, or 91%.
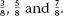
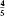
See also…
Check-up 2: Mental calculations, changing more proportions to percentages
Summary of key ideas
Per cent means ‘for each hundred’ (e.g. 35% means ‘35 out of 100’)
A proportion can be written as a percentage, by working out the equivalent number out of a hundred (e.g. ‘7 out of 20’ is ‘35 out of 100’, which is 35%; ‘240 out of 300’ is ‘80 out of 100’, which is 80%).
The percentage equivalents of many simple proportions (such as
) should be memorised.
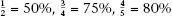
Further practice
Do these without using a calculator.
1.1
Work out the equivalent percentages for the following fractions and then commit them all to memory!
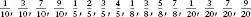
1.2
A pupil...
Table of contents
Cover Page
Title Page
Copyright Page
Contents
Read this first
Check-up 1: Mental calculations, changing proportions to percentages
Check-up 2: Mental calculations, changing more proportions to percentages
Check-up 3: Decimals and percentages
Check-up 4: Understanding data presented in tables
Check-up 5: Two-way tables for comparing two sets of data
Check-up 6: Bar charts and frequency tables for discrete data
Check-up 7: Bar charts for grouped discrete data
Check-up 8: Bar charts for continuous data
Check-up 9: Finding a fraction of a quantity
Check-up 10: Fractions to decimals and vice versa
Check-up 11: Expressing a percentage in fraction notation
Check-up 12: The commutative laws
Check-up 13: The associative laws
Check-up 14: The distributive laws
Check-up 15: Using a four-function calculator, precedence of operators
Check-up 16: Using a four-function calculator for money calculations
Check-up 17: Using the memory on a four-function calculator
Check-up 18: Using a calculator to express a proportion as a percentage
