Spectral Theory of Canonical Systems

Christian Remling

• Publisher: De Gruyter
• Year: 2018
• Print ISBN:
  9783110562026
• eBook ISBN:
  9783110562286
• Topic: Mathematics
• Subtopic: Differential Equations
• Index: Mathematics

Canonical systems occupy a central position in the spectral theory of second order differential operators. They may be used to realize arbitrary spectral data, and the classical operators such as Schrödinger, Jacobi, Dirac, and Sturm-Liouville equations can be written in this form. 'Spectral Theory of Canonical Systems' offers a selfcontained and detailed introduction to this theory. Techniques to construct self-adjoint realizations in suitable Hilbert spaces, a modern treatment of de Branges spaces, and direct and inverse spectral problems are discussed.

Contents
Basic definitions
Symmetric and self-adjoint relations
Spectral representation
Transfer matrices and de Branges spaces
Inverse spectral theory
Some applications
The absolutely continuous spectrum

1Basic definitions

1.1Canonical systems

A canonical system is a differential equation of the form

$J{u}^{\prime }\left(x\right)=-zH\left(x\right)u\left(x\right),J=\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right).\left(1.1\right)$

We consider these systems on open intervals x ∈ (a, b), possibly unbounded, so −∞ ≤ a < b ≤ ∞, and we then make the following basic assumptions on the coefficient matrix H :

(1)H(x) ∈ ℝ2×2;

(2) $H\in L_{\text{loc}}^1\left(a,b\right);$

(3)H(x) ≥ 0 for (Lebesgue) almost every x ∈ (a, b).

What I am asking for in condition (2) is that the entries of H are locally integrable functions, and similar conventions will be used in the sequel when I talk about Lp conditions on vector or matrix valued functions. Condition (3) means that for almost every x, the matrix H(x) is symmetric and v∗H(x)v ≥ 0 for all v ∈ ℂ2.

The z from (1.1) is sometimes referred to as the spectral parameter; but for now, all we need to know is that z is a complex number.

It is useful to make one more basic assumption from the outset, even though some things could be done without it. Namely, I also assume:

(4)H(x) ≠ 0 for almost every x ∈ (a, b).

If we had an interval (c, d) on which H = 0 almost everywhere, then the solutions would simply stay constant on (c, d), and removing the interval would not have any effect on the complement. If H = 0 on a more complicated positive measure set, then things are not as immediately obvious, but we could still use a transformation similar to the one discussed in Section 1.3 to remove such a set. More importantly, later results will confirm convincingly that making assumption (4) was the right choice.

The differential equation (1.1) has the general structure of an eigenvalue problem: namely, if we imagine a (formal) differential operator τ that acts on ℂ2 valued functions u as $\left(\tau u\right)(\mathrm{x...}$

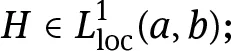
Table of contents

• Cover
• Title Page
• Copyright
• Contents
• Preface
• 1 Basic definitions
• 2 Symmetric and self-adjoint relations
• 3 Spectral representation
• 4 Transfer matrices and de Branges spaces
• 5 Inverse spectral theory
• 6 Some applications
• 7 The absolutely continuous spectrum
• Bibliography
• Index