Chancing It

The Laws of Chance and How They Can Work for You

Robert Matthews

• Publisher: Skyhorse
• Year: 2017
• ISBN:
  9781510723818
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

Make your own luck by understanding probability Over the years, some very smart people have thought they understood the rules of chance?only to fail dismally. Whether you call it probability, risk, or uncertainty, the workings of chance often defy common sense. Fortunately, advances in math and science have revealed the laws of chance, and understanding those laws can help in your everyday life. In Chancing It, award-winning scientist and writer Robert Matthews shows how to understand the laws of probability and use them to your advantage. He gives you access to some of the most potent intellectual tools ever developed and explains how to use them to guide your judgments and decisions. By the end of the book, you will know:

• How to understand and even predict coincidences
• When an insurance policy is worth having
• Why "expert" predictions are often misleading
• How to tell when a scientific claim is a breakthrough or baloney
• When it makes sense to place a bet on anything from sports to stock markets

?A groundbreaking introduction to the power of probability, Chancing It will sharpen your decision-making and maximize your luck.

The coin-tossing prisoner of the Nazis

In the spring of 1940, John Kerrich set out from his home to visit his in-laws – no small undertaking, given that he lived in South Africa and they were in Denmark 12,000 kilometres away. And the moment he arrived in Copenhagen he must have wished he’d stayed at home. Just days earlier, Denmark had been invaded by Nazi Germany. Thousands of troops swarmed over the border in a devastating demonstration of blitzkrieg. Within hours the Nazis had overwhelmed the opposition and taken control. Over the weeks that followed, they set about arresting enemy aliens and herding them into internment camps. Kerrich was soon among them.

It could have been worse. He found himself in a camp in Jutland run by the Danish government, which was, he later reported, run in a ‘truly admirable way’.1 Even so, he knew he faced many months and possibly years devoid of intellectual stimulation – not a happy prospect for this lecturer in mathematics from the University of Witwatersrand. Casting around for something to occupy his time, he came up with an idea for a mathematical project that required minimal equipment but which might prove instructive to others. He decided to embark on a comprehensive study of the workings of chance via that most basic of its manifestations: the outcome of tossing a coin.

Kerrich was already familiar with the theory developed by mathematicians to understand the workings of chance. Now, he realised, he had a rare opportunity to put that theory to the test on a lot of simple, real-life data. Then once the war was over – presuming, of course, he outlived it – he’d be able to go back to university equipped not only with the theoretical underpinning for the laws of chance, but also hard evidence for its reliability. And that would be invaluable when explaining the notoriously counter-intuitive predictions of the laws of chance to his students.

Kerrich wanted his study to be as comprehensive and reliable as possible, and that meant tossing a coin and recording the result for as long as he could bear. Fortunately, he found someone willing to share the tedium, a fellow internee named Eric Christensen. And so together they set up a table, spread a cloth on it and, with a flick of a thumb, tossed a coin about 30 centimetres into the air.

For the record, it came down tails.

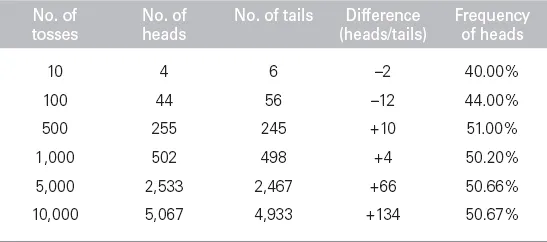
Many people probably think they could guess how things went from there. As the number of tosses increases, the well-known Law of Averages would ensure that the numbers of heads and tails would start to even out. And indeed, Kerrich found that by the 100th toss, the numbers of heads and tails were pretty similar: 44 heads versus 56 tails.

But then something odd started to happen. As the hours and coin-tosses rolled by, heads started to pull ahead of tails. By the 2,000th toss, heads had built up a lead of 26 over tails. By the 4,000th toss, the difference had more than doubled, to 58. The discrepancy seemed to be getting bigger.

By the time Kerrich called a halt – at 10,000 tosses – the coin had landed heads-up 5,067 times, exceeding the number of tails by the hefty margin of 134. Far from disappearing, the discrepancy between heads and tails had continued to grow. Was there something wrong with the experiment? Or had Kerrich discovered a flaw in the Law of Averages? Kerrich and Christensen had done their best to rule out biased tosses, and when they crunched the numbers, they found the Law of Averages had not been violated at all. The real problem was not with the coin, nor with the law, but with the commonly held view of what it says. Kerrich’s simple experiment had in fact done just what he wanted. It had demonstrated one of the big misconceptions about the workings of chance.

Asked what the Law of Averages states, many people say something along the lines of ‘In the long run, it all evens out’. As such, the law is a source of consolation when we have a run of bad luck, or our enemies seem on the ascendant. Sports fans often invoke it when on the receiving end of anything from a lost coin-toss to a bad refereeing decision. Win some, lose some – in the end, it all evens out.

Well, yes and no. Yes, there is indeed a Law of Averages at work in our universe. Its existence hasn’t merely been demonstrated experimentally; it’s been proved mathematically. It applies not only in our universe, but in every universe with the same rules of mathematics; not even the laws of physics can claim that. But no, the law doesn’t imply ‘it all evens out in the end’. As we’ll see in later chapters, precisely what it does mean took some of the greatest mathematicians of the last millennium a huge amount of effort to pin down. They still argue about the law, even now. Admittedly, mathematicians often demand a level of precision the rest of us would regard as ludicrously pedantic. But in this case, they are right to be picky. For knowing precisely what the Law of Averages says turns out to be one of the keys to understanding how chance operates in our world – and how to turn that understanding to our advantage. And the key to that understanding lies in establishing just what we mean by ‘It all evens out in the end’. In particular, what, exactly, is ‘it’?

This sounds perilously like an exercise in philosophical navel-gazing, but Kerrich’s experiment points us towards the right answer. Many people think the ‘it’ which evens out in the long run is the raw numbers of heads and tails.

So why did the coin produce far more of one outcome than another? The short answer is: because blind, random chance was acting on each coin-toss, making an exact match in the raw numbers of heads and tails ever more unlikely. So what happened to the Law of Averages? It’s alive and well; the thing is, it just doesn’t apply to the raw numbers of heads and tails. Pretty obviously, we cannot say how individual chance events will turn out with absolute certainty. But we can say something about them if we drop down to a slightly lower level of knowledge – and ask what chance events will do on average.

In the case of the coin-toss, we cannot say with certainty when we’ll get ‘heads’ or ‘tails’, or how many we’ll get of each. But given that there are just two outcomes and they’re equally likely, we can say they should pop up with equal frequency – namely, 50 per cent of the time.

And this, in turn, shows exactly what ‘it’ is that ‘evens out in the long run’. It’s not the raw numbers of heads and tails, about which we can say nothing with certainty. It is their relative frequencies: the number of times each pops up, as a proportion of the total number of opportunities we give them to do so.

This is the real Law of Averages, and it’s what Kerrich and Christensen saw at work in their experiment. As the tosses mounted up, the relative frequencies of heads and tails – that is, their numbers divided by the total number of tosses – got ever closer. By the time the experiment finished, these frequencies were within 1 per cent of being identical (50.67 per cent heads versus 49.33 per cent tails. In stark contrast, the raw numbers of heads and tails grew ever farther apart (see table).

The real Law of Averages, and what really ‘all evens out in the end’

The Law of Averages tells us that if we want to understand the action of chance on events, we should focus not on each individual event, but on their relative frequencies. Their importance is reflected in the fact they’re often regarded as a measure of that most basic feature of all chance events: their probability.

Is a coin-toss really fair?

A coin-toss is generally regarded as random, but how the coin lands can be predicted – in theory, at least. In 2008, a team from the Technical University of Łód

Poland,2 analysed the mechanics of a realistic coin tumbling under the influence of air resistance. The theory is very complex, but revealed that the coin’s behaviour is predictable until it strikes the floor. Then ‘chaotic’ behaviour sets in, with just small differences producing radically different outcomes. This in turn suggested that coin-tosses caught in mid-air may have a slight bias. This possibility has also been investigated by a team led by mathematician Persi Diaconis of Stanford University.3 They found that coins that are caught do have a slight tendency to end up in the same state as they start. The bias is, however, incredibly slight. So the outcome of tossing a coin can indeed be regarded as random, whether caught in mid-air or allowed to bounce.

So, for example, if we roll a die a thousand times, random chance is very unlikely to lead to the numbers 1 to 6 appearing precisely the same number of times; that’s a statement about individual outcomes, about which we can say nothing with certainty. But, thanks to the Law of Averages, we can expect the relative frequencies of the six different outcomes to appear in around 1/6th of all the rolls – and get ever closer to that exact proportion the more rolls we perform. That exact proportion is what we call the probability of each number appearing (though, as we’ll see later, it’s not the only way of thinking of probability). For some things – like a coin, a die or a pack of cards – we can get a handle on the probability from the fundamental properties that govern the various outcomes (the number of sides, court cards, etc.). Then we can say that, in the long run, the relative frequencies of the outcomes should get ever closer to that probability. And if they don’t, we can start to wonder about why our beliefs have proved ill-founded.

UPSHOT

The Law of Averages tells us that when we know – or suspect – we’re dealing with events that involve an element of chance, we should focus not on the events themselves, but on their relative frequency – that is, the number of times each event comes up as a proportion of the total number of opportunities to do so.

What the Law of Averages really means

The Law of Averages warns us that when dealing with chance events, it’s their relative frequencies, not their raw numbers, we should focus on. But if you’re struggling to give up the idea that it’s the raw numbers that ‘even out in the long run’, don’t beat yourself up; you’re in good company. Jean-Baptiste le Rond d’Alembert, one of the great mathematicians of the Enlightenment, was sure that a run of heads while tossing a coin made tails ever more likely.

Even today, many otherwise savvy people throw good money after bad in casinos and bookmakers in the belief that a run of bad luck makes good luck more likely. If you’re still struggling to abandon the belief, then turn the question around, and ask yourself this: why should the raw numbers of times that, say, the ball lands in red or black in roulette get ever closer as the number of spins of the wheel increases?

Think about what would be needed to bring that about. It would require the ball to keep tabs on how many times it’s landed on red and black, detect any discrepancy, and then somehow compel itself to land on either red or black to drive the numbers closer together. That’s asking a lot of a small white ball bouncing around at random.

In fairness, overcoming what mathematicians call ‘The Gambler’s Fallacy’ means overcoming the wealth of everyday experiences which seem to support it. The fact is that most of our encounters with chance are more complex than mere coin-tosses, and can easily seem to violate the Law of Averages.

For example, imagine we’re rummaging through the chaos of our sock drawer before racing off to work, looking for one of the few pairs of sensible black socks. Chances are the first few socks are hopelessly colourful. So we do the obvious thing and remove them from the drawer while we persist with our search. Now who says the Law of Averages applies, and that a run of coloured socks does not affect the chances of finding the black ones? Well, it may look vaguely similar, yet what we’re doing is wholly different from a coin-toss or a throw of the roulette ball. With the socks, we’re able to remove the outcomes we don’t like, thus boosting the proportion of black socks left in the drawer. That’s not possible with events like coi...