
- 447 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
About this book
Diese Einführung in die Logik umfaßt einen Grundkurs und einen Aufbaukurs.
Der Grundkurs ist voraussetzungsfrei geschrieben und führt in die Semantik und Beweistheorie der Aussagenlogik und elementaren Prädikatenlogik ein, eingebettet in die allgemeine Theorie des rationalen Schließens. Logische Zusammenhänge werden in Verbindung mit sorgfältig ausgewählten Übungsbeispielen – inklusive Lösungen – einsichtig gemacht. Auf die philosophische Anwendung der Logik in der logischen Rekonstruktion natursprachlicher Texte und Argumente liegt besonderes Augenmerk. Zusammenhänge zwischen alternativen logischen Notationen und Techniken, die anfangs oft Schwierigkeiten bereiten, werden sorgfältig erklärt.
Der anschließende Aufbaukurs schlägt die Brücke zwischen einer philosophischen Logikeinführung und dem fortgeschrittenen Niveau moderner formaler Logik. Nach einer gründlichen Einführung in die volle Prädikatenlogik und ihrer mengentheoretischen Semantik wendet sich der Band metalogischen Methoden zu. Prominente Resultate zur Korrektheit und Vollständigkeit der Prädikatenlogik, zur Entscheidbarkeit der monadischen und Unentscheidbarkeit der vollen Prädikatenlogik sowie zur Unvollständigkeit der Arithmetik 1. Stufe werden Schritt um Schritt erklärt.
Abgerundet wird der Band durch zahlreiche Exkurse zur philosophischen Vertiefung logischer Grundlagenfragen. Zahlreiche Übungsbeispiele mit Lösungen zum Download vertiefen den Stoff. Die Lösungen werden ab Oktober 2018 verfügbar sein.
Frequently asked questions
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Information

Teil II:Aufbaukurs in Prädikatenlogik und Metalogik
Sektion C: Fortgeschrittene Prädikatenlogik (inklusive Aussagenlogik)
13Äquivalenzumformungen in der Aussagen- und Prädikatenlogik
13.1Der aussagenlogische Äquivalenzkalkül Ä
| (DN) | A ↔ ¬¬A | Doppelte Negation |
| (Komm∧) | (A ∧ B) ↔ (B ∧ A) | Kommutativität von ∧ |
| (Komm∨) | (A ∨ B) ↔ (B ∨ A) | Kommutativität von ∨ |
| (Ass∧) | (A ∧ (B ∧ C)) ↔ ((A ∧ B) ∧ C) | Assoziativität von ∧ |
| (Ass∨) | (A ∨ (B ∨ C)) ↔ ((A ∨ B) ∨ C) | Assoziativität von ∨ |
| (Idem∧) | A ↔ (A ∧ A) | Idempotenz von ∧ |
| (Idem∨) | A ↔ (A ∨ A) | Idempotenz von ∨ |
| (Distr∧∨) | (A ∧ (B ∨ C)) ↔ ((A ∧ B) ∨ (A ∧ C)) | ∧-∨-Distributivität |
| (Distr∨∧) | (A ∨ (B ∧ C)) ↔ ((A ∨ B) ∧ (A ∨ C)) | ∨-∧-Distributivität |
| (DM∧) | ¬(A ∧ B) ↔ (¬A ∨ ¬B) | De Morgan ∧ |
| (DM∨) | ¬(A ∨ B) ↔ (¬A ∧ ¬B) | De Morgan ∨ |
| (Def→) | (A → B) ↔ (¬A ∨ B) | Bedeutung von → |
| (Def↔) | (A ↔ B) ↔ ((A → B) ∧ (B → A)) | Bedeutung von ↔ |
| (ÜbTaut) | A ∧ (B ∨ ¬B) ↔ A | Überflüssige Tautologie |
| (ÜbKont) | A ∨ (B ∧ ¬B) ↔ A | Überflüssige Kontradiktion |
| (Taut) | A ∨ (B ∨ ¬B) ↔ (C ∨ ¬C) | Tautologie |
| (Kont) | A ∧ (B ∧ ¬B) ↔ (C ∧ ¬C) | Kontradiktion |
| (Abs∧) | A ∧ (A ∨ B) ↔ A | ∧-Absorption |
| (Abs∨) | A ∨ (A ∧ B) ↔ A | ∨-Absorption |
| (GAss) | 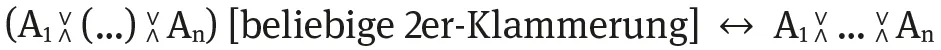 | |
| (GKomm) | 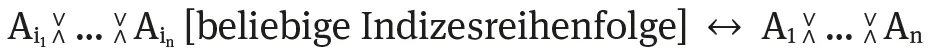 | |
| (GÜbTaut) | A ∧ (C1∨B∨C2∨¬B∨C3) ↔ A | (C1,C2,C3 können auch fehlen) |
| (GÜbKont) | A ∨ (C1∧B∧C2∧¬B∧C3) ↔ A | " |
| (GTaut) | (A1∨B∨A2∨¬B∨A3) ↔ C∨¬C | (A1,A2,A3 können auch fehlen) |
| (GKont) | (A1∧B∧A2∧¬B∧A3) ↔ C∧¬C | " |
| (GAbs∧) | A∧B∧(A∨C) ↔ A∧B | |
| (GAbs∨) | A∨B∨(A∧C) ↔ A∨B | |
| (GIdem) | 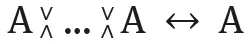 | |
| (GDistr∧∨) | (A1∨…∨Am) ∧ (B1∨…∨Bn) ↔ (A1∧B1) ∨ (A1∧B2) ∨…∨ (Am∧Bn) (m⋅n Disjunkte) | |
| (GDistr∨∧) | (A1∧…∧Am) ∨ (B1∧…∧Bn) ↔ (A1∨B1) ∧ (A1∨B2) ∧ … ∧ (Am∨Bn) (m⋅n Konjunkte) | |
| (GDM∧) | ¬(A1∧…∧An) ↔ (¬A1∨…∨¬An) | |
| (GDM∨) | ¬(A1∨…∨An) ↔ (¬A1∧…∧¬An) | |
Table of contents
- Cover
- Titelseite
- Impressum
- Vorwort
- Inhaltsverzeichnis
- Teil I: Grundkurs in Aussagenlogik und elementarer Prädikatenlogik
- Teil II: Aufbaukurs in Prädikatenlogik und Metalogik
- Literaturverzeichnis
- Symbol- und Abkürzungsverzeichnis
- Übersicht über Definitionen, Merksätze und Abbildungen
- Sachregister
- Personenregister