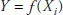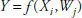Farm Business Management

The Fundamentals of Good Practice

Peter L Nuthall

• Publisher: CAB International
• Year: 2016
• Print ISBN: 9781780646572
• eBook ISBN: 9781780646596
• Topic: Technology & Engineering
• Subtopic: Agriculture
• Index: Technology & Engineering

Farming is a complex job with many unique challenges, but can also be a rich and rewarding career that is full of opportunities. Following the author's Farm Business Management series, this new textbook takes the core principles and techniques and distils them into an accessible student resource. This book: covers the most important aspects of farm management, such as observation, decision making, budgeting, risk assessment and record keeping;is organized into easy-to-navigate sections such as the farmer's environment, financials, key skills and farm systems; andincludes student-focused pedagogy throughout, comprising learning objectives, focus study exercises and review questions. Written by an expert with decades of teaching and research experience around the world, this book also incorporates two brand new chapters on farm accounting and computer systems and software. Providing a hands-on learning experience for students of agriculture, it will continue to be a much-used resource throughout their farming career.This book is enhanced with supplementary resources.

1 Introduction

Learning Objectives

• Discover the nature of farm decision problems and learn about the choices that farmers are faced with.

• Consider how to represent decision problems using symbolic models.

• Discover and recognize that farmers have varying levels of managerial ability.

• Learn about the topics the book covers and analytical methods for farm business management. What is the road ahead?

Introduction to Problem Solving

All farmers like to think they operate an optimal farming system, a system that is likely to be different from that of other farmers. Each farm is unique in its set of resources (quantity and quality) and the objectives held by the farmer and his family (note: in this book, farmers are referred to as men only in the interests of simplicity and it is acknowledged that many farmers are women). This means a particular farm’s best plan and system will be unique. For each farmer, and his advisers, the challenge is to work out this unique optimal system. Given the nature of farming and primary production, there could well be a number of near-optimal systems that for all intents and purposes can be called optimal alternatives.

This book is about the methods, techniques and ideas useful in developing improved farming systems and in improving the outcomes from the system through better managerial skills. Most of the procedures can be used by farmers themselves, and all by farm advisers and consultants.

Discussions also cover the conditions and situations that are part and parcel of farm management. The decision procedures, in general, are all about problem solving, because any decision situation implies choice and, therefore, requires a method for deciding which alternative maximizes or improves the objectives. The book does not consider the practical and technological aspects of carrying out the optimal plans, other than through considering methods of understanding and improving managerial ability.

Some decision situations might not involve risk (or more correctly, involve little risk – almost all decisions involve some degree of risk) and so the analytical method used can ignore risk. This is a much less complex approach than directly allowing for risk and therefore costs less to implement. However, in general, many farmers will want to actively allow for risk, given its intrusion into most decision problems.

While the range of potential analytical techniques available is extensive, only the commonly used approaches will be discussed. At one extreme an individual farmer might make decisions based solely on intuition, and at the other might employ someone to create complex computer-based simulation systems. In most cases, however, the latter will be too costly relative to the benefits over intuition, or over simple budgeting (a budget is an estimate of farm output from a series of farm inputs, all converted from physical terms, such as kilograms or number of animals, into costs and returns). In a budget, both the quantities and values are presented to give the net return from the particular farming system.

Problem solving can be divided into two classes: evaluative and developmental. Evaluative refers to situations in which known courses of action are being evaluated to select the best. For example, cash crop farmers might currently implement a range of crop rotation systems and need to know which is best. A farm survey might be used to solve this problem. In contrast, when new systems are being developed and tested, a developmental research situation exists. For example, the problem might be deciding how best to incorporate soybean production into a mixed cropping system in a new farming area. As known systems do not exist, these would have to be developed.

The steps to be performed in solving a problem include:

• Formulating the problem (e.g. is it one of the best stock replacement systems, or the best breed of stock, or both?).

• Constructing the model to represent the problem (e.g. developing budgets of the alternatives).

• Testing the model (e.g. comparing budget prediction with actual).

• Deriving a solution from the model (e.g. comparing budgeted profit of alternatives).

• Testing and controlling the solution (e.g. trying out the solution on part of the farm).

• Fully implementing the solution.

The rest of this immediate discussion revolves around the first two issues, after discussing the objectives in problem solving. The other steps will be covered throughout the rest of the book to a greater or lesser extent.

Optimal Solutions to Problems

A problem can be described as a situation with the following conditions:

• A farmer who has the problem: the decision maker.

• An outcome that is desired by the decision maker. If there is not a desired outcome, there is no problem because, presumably, he already has what he wants.

• At least two courses of action that have some chance of yielding the desired objective or outcome.

• An initial state of doubt in the decision maker’s mind as to which is the best course of action.

• An environment or context of the problem. The environment consists of all factors that can affect the outcome, including those not under the decision maker’s control.

Problems can be more complex than the description above. For example, perhaps the decisions taken may cause a counter reaction by others (e.g. take out a contract to capture the market), or objectives may be multi-dimensional involving several outputs (e.g. leisure hours, cash profit, environmental impacts).

Further, the answer required may not be a simple ‘do this (e.g. apply 120 kg nitrogen (N) fertilizer per hectare)’, but rather what is referred to as a strategy. This involves a rule telling the decision maker to follow one of a range of actions depending on the current state of the farm and prices (e.g. if the N price drops 10%, apply 130 kg, if it increases 15%, apply 100 kg). Similarly, a wool producer should perhaps shear his sheep in a certain month if wool prices are falling, or at a later date if they are rising. The decision depends on the current state of the environment in all senses of the word.

Formulating the Problem

One of the first steps must be to study the environment, or context, in which the problem exists. Producing a general diagram, or a description of the whole system in which the problem is embedded, can be helpful. The system will consist of objectives and potential activities satisfying these. The components are then connected by a flow of information, which leads to decisions on a choice of system or, in other words, a set of production activities.

To enable analysis, a problem must be formulated in detail. Consider each factor.

The decision maker’s objectives

Formulating objectives is difficult because farmers can seldom clearly articulate their requirements. If asked, farmers often provide general comments such as ‘(I) enjoy the farming way of life’. Such statements have little operational significance.

Thus, a consultant will have to discover the objectives and in doing so may well provide a useful service. Often a good approach is to present alternative ‘solutions’ to the problem and note the farmer’s reactions. This often reveals previously unmentioned objectives.

Sometimes, however, answers to especially prepared questions will provide a starting point (see Appendix 4) and an avenue through which to discuss objectives.

Alternative courses of action

Establishing the possibilities largely consists of:

• Identifying the variables (the factors for which decisions are required) that significantly affect the outcome of the problem (e.g. time of weaning, time of shearing, price of wool, the amount of N fertilizer to apply in a particular month).

• Determining which of the variables can be controlled directly, or indirectly, by the farmer (e.g. the price of wool cannot be controlled but time of shearing can).

In some cases none of the obvious courses of action may seem to solve the problem, and so the farmer must look for new courses of action.

Using the objectives for choosing between courses of action

Ideally, it would be good to quantify the objectives so that alternative courses of action can be given a value; choice is then easy. However, this is seldom possible for other than profit and leisure measurement. For example, the value of clearing up a stream is difficult to measure. In this case offering a range of efficient solutions to the farmer will help choice. Another example: in choosing between buying or breeding replacement stock, an adviser could estimate the cost of the best way of achieving each method and let the farmer decide on the basis of the cost and other factors, such as the risk and workload.

Models

Models of farming systems are simplified representations of the real world (Swinton and Black, 2000) in the form of numbers and symbols. Their advantage is they are easier and less costly to manipulate and experiment with than the real world. In farm management ‘symbolic models’ are used in contrast to physical models; that is, the real world is represented with symbols. For example, a simple budget.

Symbolic models

Symbolic models consist of variables representing output (e.g. profit) and input (feed, fertilizer, etc.). Thus we have, for example, a production function:

Output (Y) is some function (f) of inputs (X_i ), where a value for i represents each input (e.g. X ₁ might represent the kg of fertilizer per hectare, X ₂ = irrigation level, and so on).

Models of problem situations will always take the following form:

where Y = measure of the value of the decisions made (the output, e.g. net income, yield of crop per hectare); X_i = the variables under the control of the decision maker: the decision variables (e.g. the quantity of fertilizer/ha, the lambing date); W_j = the factors (variable or constant) that affect performance but that are not controlled by the farmer (e.g. the wool price); f = the relationship tying the variables together.

As a very simple example, the yield of wheat might be:

Yield (kg) = 5600 + 25 N, where N is the kg of nitrogen applied.

In this example it is assumed the yield will be 5600 kg/ha if no N fertilizer is used, with the yield increasing 25 kg for each kg N. In reality the relationship would be more complicated and include other variables.

In most problems there will be restrictions on the decision variables. There is, for example, usually a limited supply of fertilizer, land, working capital and all the other resources. Thus, the problem is constrained.

In constructing models, each variable has to be defined so it can be measured. Further, once the model has been constructed and validated, a method of analysis must be designed. Finally, results must be interpreted.

Considerable time may need to be spent on determining the functional relationships because these tie the model (budget) together and determine the optimal values of the decision variables. For example, how will altering the lambing date affect the lambing percentage? In budgeting the experience of the ‘budgeter’ is usually critical because this person estimates the output from the input levels assumed.

Constructing and Using Models

Models are approximations

Because of the complexity of real life, most models will only be approximations of reality. Furthermore, models need to be manageable (capable of being solved), so sometimes simplifications are necessary. (A budget is an example of a very simple model.) The problem is to decide what simplifications are reasonable. Experience helps to decide the best approach.

Possible simplification methods

Possible simplification methods include:

• Omitting decision variables (e.g. assume all lambs will be given selenium when comparing alternative stock systems).

• Simplifying uncontrolled variables (e.g. assume a given lamb price in a budget, whereas it might be any one of many prices).

• Changing the nature of variables (e.g. assume all labour comes in whole units, thus ignoring casual or part-time labour).

• Changing the constraints to a simpler form (e.g. ignoring the limitations on a cropping system imposed by having two tractors of different sizes. Simply assume the average size when developing a new programme).

Sequential decision models

Sometimes decisions are considered for a range of actions that do not all have to be implemented at once and may not need to be done for a few months (time-based models). When it comes to making some of these decisions, some of the assumptions may have changed. Thus, reconsideration may be important just before the decision is made so that all relevant up-to-date information can be used (e.g. do not decide on how much hay to sell until well into the winter).

D...

Table of contents

• Cover
• Half Title
• Title
• Copyright
• Contents
• About the Author
• List of Focus Study Exercises
• Preface
• Acknowledgements
• 1 Introduction
• 2 A Synopsis of Production Economics
• 3 The Environment Farmers Operate Under
• 4 Budgeting Theory: The Core Method of Farm Systems Analysis
• 5 Budgeting Practicalities: Costing Out the Proposals
• 6 Introduction to Managing Risk and Uncertainty
• 7 Investment Analysis: Recognizing Input–Output Timing
• 8 Farm Finances, Financial Accounts and Records in General
• 9 Skills Required
• 10 Observation Skills
• 11 Anticipation and Looking Ahead Skills
• 12 Understanding the Human Factor in Management
• 13 Decision and Management Processes and their Improvement
• 14 Improving Farming Systems Using Survey Data
• 15 Introducing Further Methods of Farm Systems Analysis
• 16 Farm Computing and Software
• 17 The Last Word: Objectives and the Family
• A1 Managerial Style Test
• A2 Managerial Aptitude Test
• A3 Question Set to Assess a Farmer's Locus of Control
• A4 Goals and Aims Question Set
• A5 Set of Questions to Assess a Farmer's Risk Attitude
• A6 The Workings of a Digital Computer
• Index
• Back Cover