Nonlinear Waves

A Geometrical Approach

Petar Popivanov, Angela Slavova

• Publisher: WSPC
• Year: 2018
• eBook ISBN: 9789813271623
• Topic: Matemáticas
• Subtopic: Ecuaciones diferenciales

This volume provides an in-depth treatment of several equations and systems of mathematical physics, describing the propagation and interaction of nonlinear waves as different modifications of these: the KdV equation, Fornberg–Whitham equation, Vakhnenko equation, Camassa–Holm equation, several versions of the NLS equation, Kaup–Kupershmidt equation, Boussinesq paradigm, and Manakov system, amongst others, as well as symmetrizable quasilinear hyperbolic systems arising in fluid dynamics.

Readers not familiar with the complicated methods used in the theory of the equations of mathematical physics (functional analysis, harmonic analysis, spectral theory, topological methods, a priori estimates, conservation laws) can easily be acquainted here with different solutions of some nonlinear PDEs written in a sharp form (waves), with their geometrical visualization and their interpretation. In many cases, explicit solutions (waves) having specific physical interpretation (solitons, kinks, peakons, ovals, loops, rogue waves) are found and their interactions are studied and geometrically visualized. To do this, classical methods coming from the theory of ordinary differential equations, the dressing method, Hirota's direct method and the method of the simplest equation are introduced and applied. At the end, the paradifferential approach is used.

This volume is self-contained and equipped with simple proofs. It contains many exercises and examples arising from the applications in mechanics, physics, optics and, quantum mechanics.

Contents:

• Introduction
• Traveling Waves and Their Profiles
• Explicit Formulas to the Solutions of Several Equations of Physics and Geometry
• First Integrals of Systems of ODE Having Jump Discontinuities
• Introduction to the Dressing Method and Application to the Cubic NLS
• Direct Methods in Soliton Theory. Hirota's Approach
• Special Type Solutions of Several Evolution PDEs
• Regularity Properties of Several Hyperbolic Equations and Systems

Readership: University and graduate students, mathematicians, physicists, engineers and specialists in the fields of evolution PDEs and their applications.Partial Differential Equations in Mathematical Physics;Traveling Waves;Solitons;Kinks;Loops;Ovals and Peakon Types;Nonlinear Waves;Rogue Waves;Evolution PDEs;Interaction of Waves;Dressing Method and Hirota's Direct Method in Studying Nonlinear Waves;Method of the Simplest Equation;Exact Solutions;Geometrical Visualization of Nonlinear Waves;Rational Solutions;Propagation of Waves and New Born Waves;Wave Front Sets of the Solutions of Nonlinear Systems of PDEs;Regularizing Properties of the Solutions of Dissipative Semilinear PDEs0 Key Features:

• Contains a competent introduction to different methods for solving and studying the properties of several evolution PDEs, namely, method of characteristics and first integrals, method of the simplest equation, dressing method, Hirota's direct method and paradifferential method
• All the solutions, their interaction and new born waves are geometrically illustrated and interpreted by 45 figures
• The treatment is self-contained and aims to accustom the readers to work on their own by including in the book a lot of examples and exercises

Chapter 1

Introduction

1.1.Introduction

We propose in this Chapter several exercises and examples of different evolution PDEs that can be considered as preparatory ones for the main part of our book. The idea is moving from examples to the essence. Some of them will introduce the reader to the construction into explicit form of soliton solutions of some model systems arising in physics. The soliton is a special solitary nonlinear wave that after a collision with another solitary wave asymptotically remains unschated. More precisely, the soliton has the same profile up to a phase change. The classical method of characteristics and the propagation and interaction of nonlinear waves is considered too. In some cases the hodograph method is useful in constructing of solutions of 2 × 2 homogeneous quasilinear systems. This approach is also included in that chapter.

We introduce also the reader to a Direct method for finding solutions (including solitons) of the Korteweg de Vries equation by using linear integral equations. Briefly, at first one solves a system of two linear PDEs L₁F = 0, L₂F = 0 and then considers a Volterra’s type linear integral equation K + F +

KFdz = 0. Each solution K(x, y, t) of the latter one gives a solution of the KdV equation by the formula u = 2

K(x, y, t). This way one can get at least theoretically a larger class of solutions of the KdV equation than can be found by the Inverse Scattering Transform too...

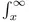
Table of contents

• Cover
• Halftitle
• Series Editors
• Title
• Copyright
• Preface
• Contents
• 1. Introduction
• 2. Traveling waves and their profiles
• 3. Explicit formulas to the solutions of several equations of physics and geometry
• 4. First integrals of systems of ODE having jump discontinuities
• 5. Introduction to the dressing method and application to the cubic NLS
• 6. Direct methods in soliton theory. Hirota’s approach
• 7. Special type solutions of several evolution PDEs
• 8. Regularity properties of several hyperbolic equations and systems
• Bibliography
• Index