
- 132 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
About this book
Written by international award-winning probability expert Henk Tijms, Basic Probability: What Every Math Student Should Know presents the essentials of elementary probability. The book is primarily written for high school and college students learning about probability for the first time. In a highly accessible way, a modern treatment of the subject is given with emphasis on conditional probability and Bayesian probability, on striking applications of the Poisson distribution, and on the interface between probability and computer simulation.
In modern society, it is important to be able to critically evaluate statements of a probabilistic nature presented in the media in order to make informed judgments. A basic knowledge of probability theory is indispensable to logical thinking and statistical literacy. The book provides this knowledge and illustrates it with numerous everyday situations.
Contents:
- Combinatorics and Calculus for Probability
- Basics of Elementary Probability
- Useful Probability Distributions with Applications
- Surprising World of Poisson Probabilities
- Computer Simulation and Probability
- Solutions to Selected Problems
Readership: High school, college and undergraduate students exposed to probability for the first time. Elementary Probability;Poisson Distribution;Bayesian Probability;Stochastic Simulation0 Key Features:
- Unique treatment of the Bayesian probability, the Poisson distribution and the interface between probability and computer simulation
- A short book that reveals the ideas with clarity and insightfulness
- The text has 97 instructive problems with answers and fully worked-out answers for a selection of 22 problems
- The student is guided in both creative and algorithmic thinking
Frequently asked questions
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app.
Information
Chapter 1
Combinatorics and Calculus for Probability
1.1 Factorials and binomial coefficients
Factorials and permutations

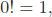
Table of contents
- Cover page
- Title page
- Copyright
- Preface
- Contents
- Chapter 1. Combinatorics and Calculus for Probability
- Chapter 2. Basics of Elementary Probability
- Chapter 3. Useful Probability Distributions with Applications
- Chapter 4. Surprising World of Poisson Probabilities
- Chapter 5. Computer Simulation and Probability
- Solutions to Selected Problems
- Index