Stochastic PDEs and Modelling of Multiscale Complex System

Xiaopeng Chen, Yan Lv;Wei Wang

• Publisher: WSPC
• Year: 2019
• eBook ISBN: 9789811200366
• Topic: Mathematics
• Subtopic: Probability & Statistics
• Index: Mathematics

This volume is devoted to original research results and survey articles reviewing recent developments in reduction for stochastic PDEs with multiscale as well as application to science and technology, and to present some future research direction. This volume includes a dozen chapters by leading experts in the area, with a broad audience in mind. It should be accessible to graduate students, junior researchers and other professionals who are interested in the subject. We also take this opportunity to celebrate the contributions of Professor Anthony J Roberts, an internationally leading figure on the occasion of his 60th years birthday in 2017.

Contents:

• Preface
• A Biographical Note and Tribute to Anthony Roberts on His 60th Birthday
• Geometric Methods for Stochastic Dynamical Systems (Jinqiao Duan and Hui Wang)
• Stochastic 3D Navier–Stokes Equations with Nonlinear Damping: Martingale Solution, Strong Solution and Small Time LDP (Hongjun Gao and Hui Liu)
• Model Reduction in Stochastic Environments (E Forgoston, L Billings and I B Schwartz)
• An Averaging Principle for Multi-valued Stochastic Differential Equations Driven by G -Brownian Motion (Yong Xu, Min Han and Bin Pei)
• Optimal Control for the Nonlocal Backward Heat Equation (Xiaoli Wang, Jinchun He, Haoyuan Xu and Meihua Yang)
• Hölder Estimates for Solutions of Stochastic Nonlocal Diffusion Equations (Guangying Lv, Hongjun Gao, Jinlong Wei, Jiang-Lun Wu)
• Multiscale Modelling Couples Patches of Two-Layer Thin Fluid Flow (Meng Cao and A J Roberts)
• The Cauchy Problem for a Generalized Ostrovsky Equation with Positive Dispersion (Wei Yan)
• Well-Posedness for Stochastic Two Component Dullin-Gottwald-Holm System with Lévy Noise (Yong Chen and Jingyun Luo)
• On Smooth Approximation of Lévy Processes in Skorokhod Space (Lingyu Feng, Xianming Liu)
• Error Estimation on Projective Integration of Expensive Multiscale Stochastic Simulation (Xiaopeng Chen and A J Roberts)
• Approximation for Stochastic Wave Equations with Singular Perturbation (Yan Lv and Wei Wang)

Readership: Students and researchers.Stochastic PDEs;Multiscale Modelling;Multiscale Stochastic Simulation;Stochastic Averaging;Model Reduction;Optimal Control;Stochastic Nonlocal Diffusion00

Chapter 1

Geometric Methods for Stochastic Dynamical Systems

Jinqiao Duan¹,* and Hui Wang^2,†

¹Department of Applied Mathematics, Illinois Institute of Technology, Chicago, IL 60561, USA
²School of Mathematics and Statistics, Zhengzhou University, Zhengzhou 450001, China
*[email protected]; ^†[email protected]

1.Introduction

Noisy fluctuations are ubiquitous in complex systems. They play a crucial or delicate role in the dynamical evolution of gene regulation, signal transduction, biochemical reactions, among other systems. Therefore, it is essential to consider the effects of noise on dynamical systems. It has been a challenging topic to have better understanding of the impact of the noise on the dynamical behaviors of complex systems. See [1, 2] for more information.

1.1.Stochastic dynamical systems

A dynamical system may be thought as evolution of mechanical ‘particles’, and is then described by a system of ordinary differential equations

where f is often called a vector field. In natural science and applied science, the dynamical systems are used to describe the evolution of complex phenomena [3–5]. However, dynamical systems are often influenced by random factors in the environment, such as in the systems of the propagation of waves through random media, stochastic particle acceleration, signal detection, and optimal control with fluctuating constraints. Indeed, a small random disturbance may have an unexpected effect on the whole dynamical system. A stochastic dynamical system is a dynamical system with noisy components or under random influences [1, 2] and thus may be modeled by a stochastic differential equation

Usually, we use two kinds of noise. One is Gaussian noise, and the other is non-Gaussian noise. Gaussian noise is modeled by Brownian motion B_t, while non-Gaussian noise is expressed via Lévy process (especially α-stable Lévy motion

) [6, 7]. Dynamical systems driven by Gaussian noise have been widely studied, but in some complex systems, the random influences or stochastic processes are non-Gaussian. For example, during the regulation of gene expression, transcriptions of DNA from genes and translations into proteins take place in a bursty, intermittent, unpredictable manner [8–13]. It is more suitable to model these processes by dynamical systems with non-Gaussian Lévy noise.

In order to better describe the impact of noise on the dynamical systems, we consider some geometric methods. These include most probable phase portraits, mean phase portraits, invariant manifolds, and slow manifolds. These geometric tools may help us characterize the impact of noise on the dynamical systems vividly from the geometric perspective.

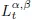
2.Stochastic dynamial systems

Consider a stochastic dynamical system in n-dimensional Euclidean space

ⁿ, either with (Gaussian) Brownian noise

or (non-Gaussian) Lévy noise

where σ is noise intensity. Let us briefly recall the definition of Brownian motion and Lévy motion.

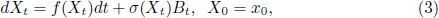
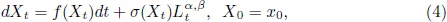
2.1.Brownian motion

Definition ([14]) A Brownian motion B_t is a stochastic process defined on a probability space Ω equipped with probability

, with the following properties:

(i) B₀ = 0, almost surely;

(ii) B_t has independent increments;

(iii) B_t has stationary increments with normal distribution: B_t – B_s ∼

(t – s, 0), for t > s;

(iv) B_t has continuous sample paths, almost surely.

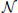
2.2.Lévy motion

Definition ([2]) On a sample space Ω equipped with probability

, a scalar asymmetric stable Lévy motion

, with the non-Gaussianity index α ∈ (0, 2) and the skewness index β ∈ [−1, 1], is a stochastic process with the following properties:

(i)

, almost surely;

(ii)

has independent increments;

(iii)

has stationary increments with stable distribution:

, β, 0), for t > s;

(iv)

has stochastically continuous sample paths, i.e., for every s,

in probability (i.e., for all δ > 0,

), as t → s.

The jump measure, which describes jump intensity and size for sample paths, for the a...

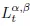
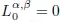
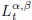
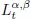
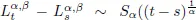
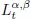
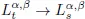
Table of contents

• Cover Page
• Title Page
• Copyright Page
• Preface
• A Biographical Note and Tribute to Anthony Roberts on His 60th Birthday
• Contents
• 1. Geometric Methods for Stochastic Dynamical Systems
• 2. Stochastic 3D Navier–Stokes Equations with Nonlinear Damping: Martingale Solution, Strong Solution and Small Time LDP
• 3. Model Reduction in Stochastic Environments
• 4. An Averaging Principle for Multi-valued Stochastic Differential Equations Driven by G-Brownian Motion
• 5. Optimal Control for the Nonlocal Backward Heat Equation
• 6. Hölder Estimates for Solutions of Stochastic Nonlocal Diffusion Equations
• 7. Multiscale Modelling Couples Patches of Two-Layer Thin Fluid Flow
• 8. The Cauchy Problem for a Generalized Ostrovsky Equation with Positive Dispersion
• 9. Well-Posedness for Stochastic Two Component Dullin–Gottwald–Holm System with Lévy Noise
• 10. On Smooth Approximation of Lévy Processes in Skorokhod Space
• 11. Error Estimation on Projective Integration of Expensive Multiscale Stochastic Simulation
• 12. Approximation for Stochastic Wave Equations with Singular Perturbation