Optimization for Engineering Problems

Kaushik Kumar, J. Paulo Davim, Kaushik Kumar, J. Paulo Davim

• Publisher: Wiley-ISTE
• Year: 2019
• Print ISBN: 9781786304742
• eBook ISBN: 9781119644613
• Edition: 1
• Topic: Tecnología e ingeniería
• Subtopic: Ingeniería eléctrica y telecomunicaciones

Optimization is central to any problem involving decision-making in engineering. Optimization theory and methods deal with selecting the best option regarding the given objective function or performance index. New algorithmic and theoretical techniques have been developed for this purpose, and have rapidly diffused into other disciplines. As a result, our knowledge of all aspects of the field has grown even more profound. In Optimization for Engineering Problems, eminent researchers in the field present the latest knowledge and techniques on the subject of optimization in engineering. Whereas the majority of work in this area focuses on other applications, this book applies advanced and algorithm-based optimization techniques specifically to problems in engineering.

1
Review of some Constrained Optimization Schemes

With rapid breakthroughs in the metaheuristic optimization methods in recent times, applications of conventional optimization solution techniques have been reduced. However, in some cases, where the computational issues are of major concern, these standard schemes are still in use. Modification to these core approaches can be appropriately incorporated to handle them more effectively. This chapter summarizes the existing important constrained optimization schemes. Many engineering problems are usually multi-objective in nature. Even though several solution approaches are available; a unified method is always preferred to solve such problems. This chapter will review some direct solution schemes including complex search, random search and method of feasible directions, and their performance in terms of accuracy, computational requirements and time at par with commonly used modern heuristic algorithms.

1.1. Introduction

In computer-aided design (CAD), optimization plays an important role. Optimization problems arise in many areas of engineering, including product design and operational control. Unit cells of atoms in metals and alloys, honeycomb structures and genetic operations are some examples of optimized systems in real life. Depending on the objective function and constraints, different types of optimization problems often arise. After Cauchy invented the gradient concept of a function in 1847, several other researchers, including Dantzig (simplex method, 1951), Kuhn–Tucker (conditions of optimality, 1951), Rosen (gradient projection method, 1960), and Fletcher and Reeves (conjugate gradient scheme, 1964), have initiated the foundation for obtaining solutions of complex linear and nonlinear optimization problems. Today, optimization techniques are widely used in operations research and industrial engineering problems, such as inventory control, scheduling and facilities design. Some of the developments in this line are linear programming, sequential quadratic programming, integer programming, dynamic programming (Bellman 1952) and geometric programming (Duffin 1967).

The mathematical problem of constrained systems is to simultaneously consider the attainment of objective function and the satisfaction of constraints. Constraints are either of the geometric type or simply the side constraints in the form of variable bounds. The effective objective function therefore first searches for the feasible solution rather than the optimum solution. All the methods start with finding feasible solutions and then move towards the optimum value. This chapter presents a review of a few techniques of obtaining optimum solutions for constrained nonlinear programming problems and attempts to identify their benefits and difficulties over heuristic methods such as simulated annealing. A few methods to handle multi-objective optimization problems are also briefly explained.

1.2. Constrained optimization problems

The constrained optimization problem in general can be stated as:

[1.1]

where X = [x₁, x₂, … x_D]^T ∈R^D is a set of design variables, while x_iL and x_iR are the lower and upper boundaries (limits) of the variable x_i, respectively. When both the objective function and constraints are linear functions of X, it is said to be a linear programming problem (e.g. cost minimization with demand (resource) constraints). Similarly, when the objective function is quadratic, while the constraints are linear, it forms a quadratic programming problem. In general, the feasible optimum solution for a nonlinear programming problem with constraints can be obtained from two broad categories of methods, namely direct and indirect methods. In direct methods, constraints are handled explicitly, while in indirect approaches, the problem is solved as a sequence of unconstrained minimization problems. Techniques such as random search, heuristic search methods and Rosen’s gradient project scheme come under direct methods, whereas penalty function methods come under indirect methods. In general, constraints have no effect on the optimum solution. In most of the problems, satisfaction of all the constraints is a mandatory requirement for the optimum solution. Therefore, often a feasible solution satisfying all the constraints is first estimated and then tested for optimality. Usually, the optimum solution occurs on the constraint boundaries.

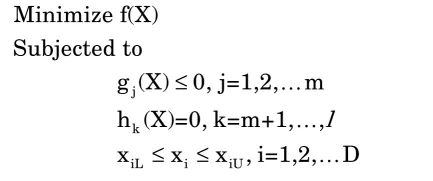
1.3. Direct solution techniques

In direct search methods for constrained minimization, the structure of constraints is employed. The main advantage of such methods is handling of discontinuous and non-differentiable functions. Some of these techniques are more or less heuristic in nature, which have no convergence proofs. Essentially, these methods start with a feasible point and a new point is created using a fixed transition rule from the chosen initial point. If the new point is infeasible, then the point is not accepted and another point is found again using the transition rule. If the new point is feasible and better than the previous point, then the point is accepted and the next iteration is performed from the new point. The process is continued until some termination criterion is met.

1.3.1. Complex search method

The Box complex method is a numerical multi-start constrained optimization algorithm developed by Box (1965). Even though this method cannot handle equality constraints, it works nicely for most design engineering problems. It assumes that an initial feasible point X (satisfying all m constraints) is available. The approach is ...

Table of contents

• Cover
• Table of Contents
• Preface
• 1 Review of some Constrained Optimization Schemes
• 2 Application of Flower Pollination Algorithm for Optimization of ECM Process Parameters
• 3 Machinability and Multi-response Optimization of EDM of Al7075/SIC/WS2 Hybrid Composite Using the PROMETHEE Method
• 4 Optimization of Cutting Parameters during Hard Turning using Evolutionary Algorithms
• 5 Development of a Multi-objective Salp Swarm Algorithm for Benchmark Functions and Real-world Problems
• 6 Water Quality Index: is it Possible to Measure with Fuzzy Logic?
• List of Authors
• Index
• End User License Agreement