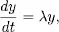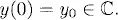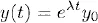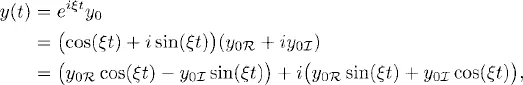Introduction to Numerical Methods for Time Dependent Differential Equations

Heinz-Otto Kreiss, Omar Eduardo Ortiz

• Publisher: Wiley
• Year: 2014
• ISBN:
  9781118838914
• Edition: 1
• Topic: Matemáticas
• Subtopic: Análisis matemático

Introduces both the fundamentals of time dependent differential equations and their numerical solutions

Introduction to Numerical Methods for Time Dependent Differential Equations delves into the underlying mathematical theory needed to solve time dependent differential equations numerically. Written as a self-contained introduction, the book is divided into two parts to emphasize both ordinary differential equations (ODEs) and partial differential equations (PDEs).

Beginning with ODEs and their approximations, the authors provide a crucial presentation of fundamental notions, such as the theory of scalar equations, finite difference approximations, and the Explicit Euler method. Next, a discussion on higher order approximations, implicit methods, multistep methods, Fourier interpolation, PDEs in one space dimension as well as their related systems is provided.

Introduction to Numerical Methods for Time Dependent Differential Equations features:

• A step-by-step discussion of the procedures needed to prove the stability of difference approximations
• Multiple exercises throughout with select answers, providing readers with a practical guide to understanding the approximations of differential equations
• A simplified approach in a one space dimension
• Analytical theory for difference approximations that is particularly useful to clarify procedures

Introduction to Numerical Methods for Time Dependent Differential Equations is an excellent textbook for upper-undergraduate courses in applied mathematics, engineering, and physics as well as a useful reference for physical scientists, engineers, numerical analysts, and mathematical modelers who use numerical experiments to test designs or predict and investigate phenomena from many disciplines.

PART I

ORDINARY DIFFERENTIAL EQUATIONS AND THEIR APPROXIMATIONS

CHAPTER 1

FIRST-ORDER SCALAR EQUATIONS

In this chapter we study the basic properties of first-order scalar ordinary differential equations and their solutions. The first and larger part is devoted to linear equations and various of their basic properties, such as the principle of superposition, Duhamel’s principle, and the concept of stability. In the second part we study briefly nonlinear scalar equations, emphasizing the new behaviors that emerge, and introduce the very useful technique known as the principle of linearization. The scalar equations and their properties are crucial to an understanding of the behavior of more general differential equations.

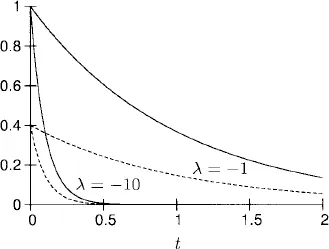
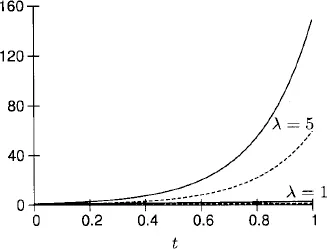
1.1 Constant coefficient linear equations

Consider a complex function y of a real variable t. One of the simplest differential equations that y can obey is given by

(1.1)

where λ

is constant. We want to solve the initial value problem, that is, we want to determine a solution for t ≥ 0 with given initial value

(1.2)

Clearly,

(1.3)

is the solution of (1.1), (1.2). Let us discuss the solution under different assumptions for the λ constant. In Figures 1.1 and 1.2 we illustrate the solution for y₀ = 1+0.4i and different values of λ.

Figure 1.1 Exponentially decaying solutions. Re y shown as solid lines and Im y as dashed lines.

Figure 1.2 Exponentially growing solutions. Re y is shown as solid line and Im y as a dashed line.

1. λ

, λ < 0. In this case both the real and imaginary parts of the solution decay exponentially. If |λ|

1, the decay is very rapid.

2. λ

, λ > 0. The solution grows exponentially. The growth is slow if |λ|

1. For example, for λ = 0.01 we have, by Taylor expansion,

On the other hand, if λ

1, the solution grows very rapidly.

3. λ = i

, ξ

. In this case, the amplitude |y(t)| of the solution is constant in time,

If the complex initial data y₀ is written as

the solution is

which defines the real part y

(t) and imaginary part y

(t) of the solution. Both parts are oscillatory functions of t. The solution is highly oscillatory if |ξ|

1. Figure 1.3 shows the solution for ...