Calculus Essentials For Dummies

Mark Ryan

• Publisher: For Dummies
• Year: 2019
• Print ISBN: 9781119591207
• eBook ISBN: 9781119591221
• Edition: 1
• Topic: Mathematics
• Subtopic: Calculus
• Index: Mathematics

Calculus Essentials For Dummies (9781119591207) was previously published as Calculus Essentials For Dummies (9780470618356). While this version features a new Dummies cover and design, the content is the same as the prior release and should not be considered a new or updated product.

Many colleges and universities require students to take at least one math course, and Calculus I is often the chosen option. Calculus Essentials For Dummies provides explanations of key concepts for students who may have taken calculus in high school and want to review the most important concepts as they gear up for a faster-paced college course. Free of review and ramp-up material, Calculus Essentials For Dummies sticks to the point with content focused on key topics only. It provides discrete explanations of critical concepts taught in a typical two-semester high school calculus class or a college level Calculus I course, from limits and differentiation to integration and infinite series. This guide is also a perfect reference for parents who need to review critical calculus concepts as they help high school students with homework assignments, as well as for adult learners headed back into the classroom who just need a refresher of the core concepts.

The Essentials For Dummies Series
Dummies is proud to present our new series, The Essentials For Dummies. Now students who are prepping for exams, preparing to study new material, or who just need a refresher can have a concise, easy-to-understand review guide that covers an entire course by concentrating solely on the most important concepts. From algebra and chemistry to grammar and Spanish, our expert authors focus on the skills students most need to succeed in a subject.

Chapter 1

Calculus: No Big Deal

IN THIS CHAPTER

Calculus — it’s just souped-up regular math

Zooming in is the key

Delving into the derivative: It’s a rate or a slope

Investigating the integral — addition for experts

In this chapter, I answer the question “What is calculus?” in plain English and give you real-world examples of how it’s used. Then I introduce you to the two big ideas in calculus: differentiation and integration. Finally, I explain why calculus works. After reading this chapter, you will understand what calculus is all about.

So What Is Calculus Already?

Calculus is basically just very advanced algebra and geometry. In one sense, it’s not even a new subject — it takes the ordinary rules of algebra and geometry and tweaks them so that they can be used on more complicated problems. (The rub, of course, is that darn other sense in which it is a new and more difficult subject.)

Look at Figure 1-1. On the left is a man pushing a crate up a straight incline. On the right, the man is pushing the same crate up a curving incline. The problem, in both cases, is to determine the amount of energy required to push the crate to the top. You can do the problem on the left with regular math. For the one on the right, you need calculus (if you don’t know the physics shortcuts).

FIGURE 1-1: The difference between regular math and calculus: In a word, it’s the curve.

For the straight incline, the man pushes with an unchanging force, and the crate goes up the incline at an unchanging speed. With some simple physics formulas and regular math (including algebra and trig), you can compute how many calories of energy are required to push the crate up the incline. Note that the amount of energy expended each second remains the same.

For the curving incline, on the other hand, things are constantly changing. The steepness of the incline is changing — and it’s not like it’s one steepness for the first 3 feet and then a different steepness for the next 3 — it’s constantly changing. And the man pushes with a constantly changing force — the steeper the incline, the harder the push. As a result, the amount of energy expended is also changing, not just every second or thousandth of a second, but constantly, from one moment to the next. That’s what makes it a calculus problem. It should come as no surprise to you, then, that calculus is called “the mathematics of change.” Calculus takes the regular rules of math and applies them to fluid, evolving problems.

For the curving incline problem, the physics formulas remain the same, and the algebra and trig you use stay the same. The difference is that — in contrast to the straight incline problem, which you can sort of do in a single shot — you’ve got to break up the curving incline problem into small chunks and do each chunk separately. Figure 1-2 shows a small portion of the curving incline blown up to several times its size.

FIGURE 1-2: Zooming in on the curve — voilà, it’s straight (almost).

When you zoom in far enough, the small length of the curving incline becomes practically straight. Then you can solve that small chunk just like the straight incline problem. Each small chunk can be solved the same way, and then you just add up all the chunks.

That’s calculus in a nutshell. It takes a problem that can’t be done with regular math because things are constantly changing — the changing quantities show up on a graph as curves — it zooms in on the curve till it becomes straight, and then it finishes off the problem with regular math.

What makes calculus such a fantastic achievement is that it does what seems impossible: it zooms in infinitely. As a matter of fact, everything in calculus involves infinity in one way or another, because if something is constantly changing, it’s changing infinitely often from each infinitesimal moment to the next.

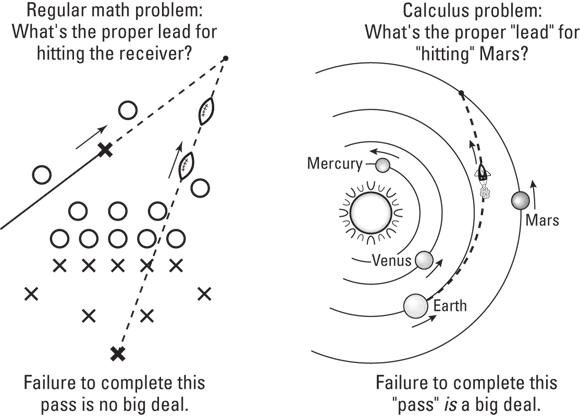
Real-World Examples of Calculus

So, with regular math you can do the straight incline problem; with calculus you can do the curving incline problem. With regular math you can determine the length of a buried cable that runs diagonally from one corner of a park to the other (remember the Pythagorean Theorem?). With calculus you can determine the length of a cable hung between two towers that has the shape of a catenary (which is different, by the way, from a simple circular arc or a parabola). Knowing the exact length is of obvious importance to a power company planning hundreds of miles of new electric cable.

You can calculate the area of the flat roof of a home with regular math. With calculus you can compute the area of a complicated, nonspherical shape like the dome of the Minneapolis Metrodome. Architects need to know the dome’s area to determine the cost of materials and to figure the weight of the dome (with and without snow on it). The weight, of course, is needed for planning the strength of the supporting structure.

With regular math and simple physics, you can calculate how much a quarterback must lead a pass receiver if the receiver runs in a straight line and at a constant speed. But when NASA, in 1975, calculated the necessary “lead” for aiming the Viking I at Mars, it needed calculus because both the Earth and Mars travel on elliptical orbits, and the speeds of both are constantly changing — not to mention the fact that on its way to Mars, the spacecraft was affected by the different and constantly changing gravitational pulls of the Earth, moon, Mars, the sun. See Figure 1-3.

FIGURE 1-3: B.C.E. (Before the Calculus Era) and C.E. (the Calculus Era).

Differentiation

Differentiation is the first big idea in calculus. It’s the process of finding a derivative of a curve. And a deriva...

Table of contents

• Cover
• Table of Contents
• Introduction
• Chapter 1: Calculus: No Big Deal
• Chapter 2: Limits and Continuity
• Chapter 3: Evaluating Limits
• Chapter 4: Differentiation Orientation
• Chapter 5: Differentiation Rules
• Chapter 6: Differentiation and the Shape of Curves
• Chapter 7: Differentiation Problems
• Chapter 8: Introduction to Integration
• Chapter 9: Integration: Backwards Differentiation
• Chapter 10: Integration for Experts
• Chapter 11: Using the Integral to Solve Problems
• Chapter 12: Eight Things to Remember
• Index
• About the Author
• Advertisement Page
• Connect with Dummies
• End User License Agreement