Introduction to Dynamics and Control in Mechanical Engineering Systems

Cho W. S. To

• Publisher: Wiley-ASME Press Series
• Year: 2016
• Print ISBN: 9781118934920
• eBook ISBN: 9781118934913
• Edition: 1
• Topic: Technology & Engineering
• Subtopic: Mechanical Engineering
• Index: Technology & Engineering

One of the first books to provide in-depth and systematic application of finite element methods to the field of stochastic structural dynamics
The parallel developments of the Finite Element Methods in the 1950's and the engineering applications of stochastic processes in the 1940's provided a combined numerical analysis tool for the studies of dynamics of structures and structural systems under random loadings. In the open literature, there are books on statistical dynamics of structures and books on structural dynamics with chapters dealing with random response analysis. However, a systematic treatment of stochastic structural dynamics applying the finite element methods seems to be lacking. Aimed at advanced and specialist levels, the author presents and illustrates analytical and direct integration methods for analyzing the statistics of the response of structures to stochastic loads. The analysis methods are based on structural models represented via the Finite Element Method. In addition to linear problems the text also addresses nonlinear problems and non-stationary random excitation with systems having large spatially stochastic property variations.

1
Introduction

This book is concerned with the introduction to the dynamics and controls of engineering systems in general. The emphasis, however, is on mechanical engineering system modeling and analysis.

• Dynamics is a branch of mechanics and is concerned with the studies of particles and bodies in motion.
• The term control refers to the process of modifying the dynamic behavior of a system in order to achieve some desired outputs.
• A system is a combination of components or elements so constructed to achieve an objective or multiple objectives.

1.1 Important Difference between Static and Dynamic Responses

The question of why one studies engineering dynamics as well as control, and not statics, is best answered by the fact that in control engineering it is the dynamic behavior of a system that is modified instead of the static one. Furthermore, the most important difference between statics and dynamics from the point of view of a mechanical engineering designer is in the responses of a system to an applied force.

Consider a lightly damped, simple, single degree-of-freedom (dof) system that is subjected to a unit step load. The dynamic response is shown in Figure 1.1. Note that the largest peak or overshoot is about 1.75 units, while the magnitude of the input is 1.0 unit. Owing to the positive damping in the system, the dynamic response approaches asymptotically to its steady-state (s.s.) value of unity. If one looks at the largest mean square value for the dynamic response, it is about 3.06 units squared. On the other hand, the mean square value for the s.s. or static response is 1.0 unit squared. Thus, the largest mean square value, which is the main design parameter, for the dynamic case is about 306% that of the static case, indicating the importance of dynamic response compared with that of the static case.

Figure 1.1 Dynamic response of a single dof system under unity input

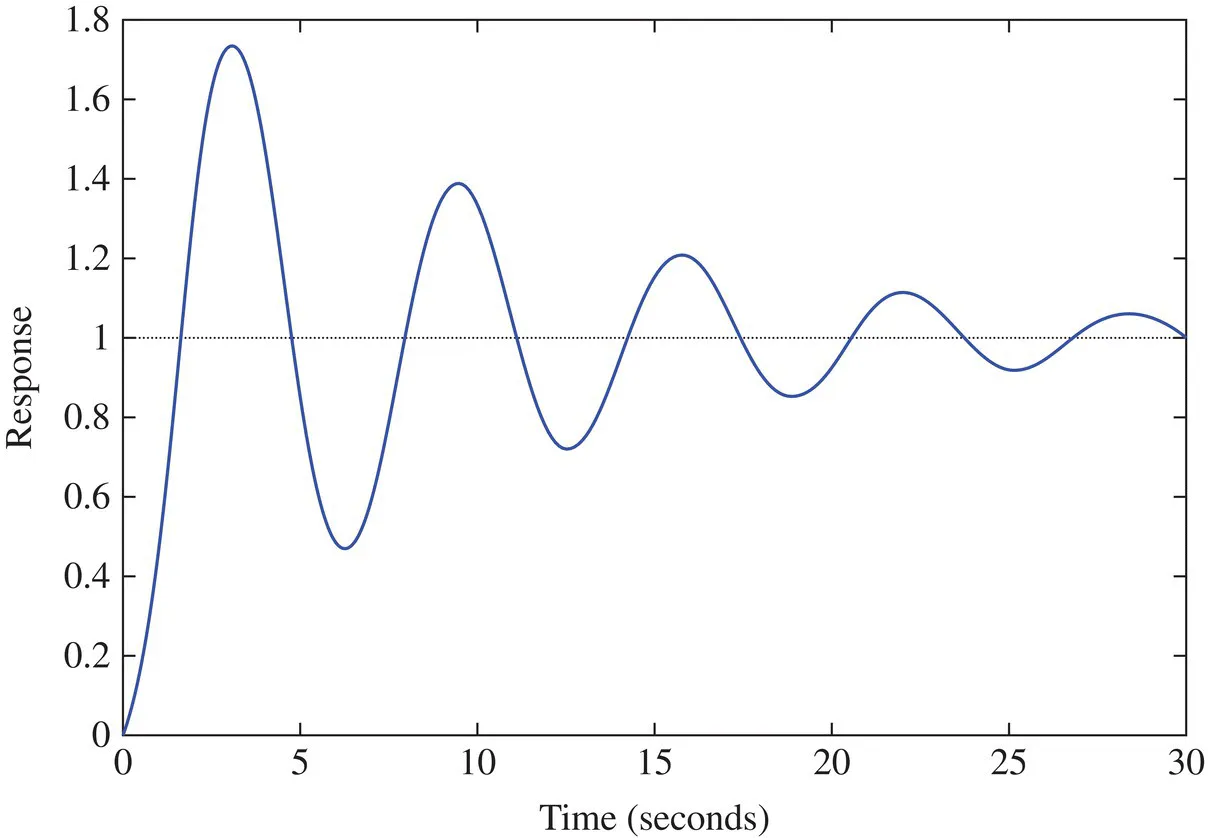
1.2 Classification of Dynamic Systems

This book deals with the study of dynamic and control systems in the engineering or physical world. In the latter many phenomena are nonlinear and random in nature, and therefore to describe, study, and understand such phenomena one has to formulate these phenomena in the conceptual or mathematical world as nonlinear differential equations. The latter, apart from some special cases, are generally very difficult to solve mathematically, and therefore in many situations these nonlinear differential equations are simplified to linear differential equations such that they may be solved analytically or numerically.

The meaning of a linear phenomenon may better be understood by considering a simple uniform cantilever beam of length L under a dynamic point load f(t) applied transversely at the tip as shown in Figure 1.2. If the tip deflection y(L,t), or simply written as y, satisfies the condition that

then y is said to be linear, and therefore a linear differential equation can be used to describe the deflection y. If the deflection y is larger than 5% of the length L of the beam, a nonlinear differential equation has to be employed instead. The word random mentioned in the foregoing means that statistical analysis is required to study such phenomena, instead of the usual deterministic approaches that are employed throughout in this book.

Figure 1.2 Cantilever beam with a point load

For the cantilever beam shown in Figure 1.2, the transverse deflection y at any point x along the length of the beam is a function of space x and time t, and therefore the differential equation required to describe the deflection is a partial differential equation (p.d.e.). Such a system is referred to as continuous. Continuous systems are also known as distributed parameter models and they possess an infinite number of dof.

On the other hand, for simplicity, if one approximates the uniform cantilever beam as massless such that the elasticity of the beam may be considered as a spring of constant coefficient k = 3EI/L³, where E is the Young’s modulus of elasticity of the material and I the second moment of cross-sectional area of the beam, and the mass of the beam m is considered concentrated at the tip of the beam, then the dynamic deflection of this discrete or lumped-parameter model, shown in Figure 1.3, can be described by an ordinary differential equation (o.d.e.).

Figure 1.3 A lumped-parameter model of a massless cantilever beam

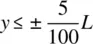
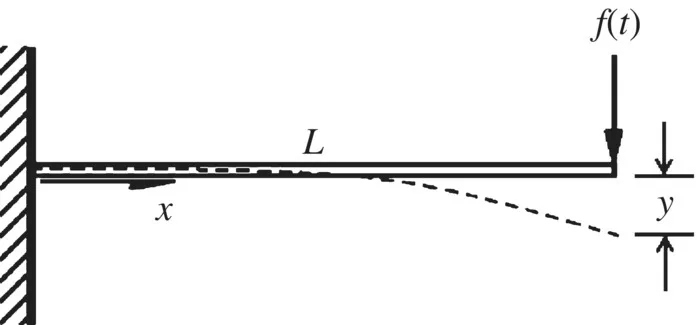
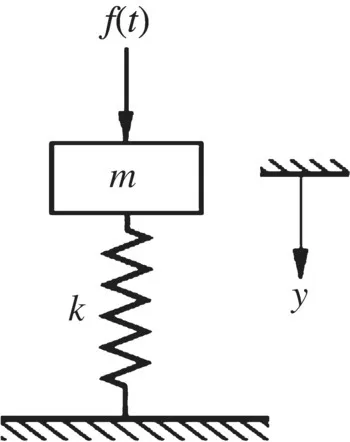
1.3 Applications of Control Theory

It is believed that the first use of automatic control in Western civilization dated back to the period of 300 BC [1]. In the Far East the best-known automatic control in ancient China is the south-pointing chariot [1].

Fast forward to 1922, when Minorsky [2] introduced his three-term controller for the steering of ships, thereby becoming the first to use the proportional, integral, and derivative (PID) controller. In this publication [2] he also considered nonlinear effects in the closed-loop system (to be defined in Chapter 8). In modern times the theory of control has been applied in many fields. The following representative applications are im...

Table of contents

• Cover
• Title Page
• Table of Contents
• Series Preface
• Preface
• Acknowledgments
• 1 Introduction
• 2 Review of Laplace Transforms
• 3 Dynamic Behaviors of Hydraulic and Pneumatic Systems
• 4 Dynamic Behaviors of Oscillatory Systems
• 5 Formulation and Dynamic Behavior of Thermal Systems
• 6 Formulation and Dynamic Behavior of Electrical Systems
• 7 Dynamic Characteristics of Transducers
• 8 Fundamentals of Control Systems
• 9 Analysis and Performance of Control Systems
• 10 Stability Analysis of Control Systems
• 11 Graphical Methods for Control Systems
• 12 Modern Control System Analysis
• Index
• End User License Agreement