Banach, Fréchet, Hilbert and Neumann Spaces

Jacques Simon

• Publisher: Wiley-ISTE
• Year: 2017
• Print ISBN: 9781786300096
• eBook ISBN: 9781119426530
• Edition: 1
• Topic: Matematica
• Subtopic: Matematica generale

This book is the first of a set dedicated to the mathematical tools used in partial differential equations derived from physics.

Its focus is on normed or semi-normed vector spaces, including the spaces of Banach, Fréchet and Hilbert, with new developments on Neumann spaces, but also on extractable spaces.

The author presents the main properties of these spaces, which are useful for the construction of Lebesgue and Sobolev distributions with real or vector values and for solving partial differential equations. Differential calculus is also extended to semi-normed spaces.

Simple methods, semi-norms, sequential properties and others are discussed, making these tools accessible to the greatest number of students – doctoral students, postgraduate students – engineers and researchers without restricting or generalizing the results.

Chapter 1
Prerequisites

The purpose of this preliminary chapter is to clarify terminology and notation and to recall elementary properties of countability and of real numbers. The heart of the matter begins in Chapter 2, p. 11.

1.1. Sets, mappings, orders

Set theory notations. We utilize the usual notations of set theory¹, namely = for “is equal to”, ∈ for “is an element of”, ∀ for “for all”, ∃ for “there exists”, ⇒ for “implies”, ⇐ for “results from”, ⇔ for “is equivalent to”. A barred symbol designates the negation of the property, for example ≠ means “is not equal to”.

We denote {a, b, …, z} the set consisting of a, b, … and z, {a : P(a)} or {a}_P(a) the set of the a having the property P(a), and ∅ the empty set. We denote ⊂ set inclusion, ∩ their union and ∩ their intersection. We denote ⊃ for “is a superset of” and U \ V = {u ∈ U : u ∉ V}.

We denote (a, b, …, z) the ordered set composed of a, b, … and z. Therefore, (a, b) ≠ (b, a) if a≠ b. On the contrary, {a, b} = {b, a} always holds.

We denote U₁× U₂× ·· × U_d = { (u₁, u₂, …, u_d) : u_i ∈ U_i for all i} the product² of the sets U₁,… , U_d and denote U^d = { (u₁, u₂, …, u_d) : u_i ∈ U for every i}. In particular, U² = U × U.

Given a set I and for each i ∈ I, a set U_i, we denote ⋃_{i ∈I} U_i the union of all the U_i, ⋂_{i ∈ I} U_i their intersection and ∏_{i ∈ I} U_i = {(u_i)_{i ∈ I}:u_i ∈ U_i, ∀ i ∈ I} their product. These quantities are related by De Morgan’s laws³:

(1.1)

(1.2)

The axiomatic construction of the set theory is, for instance, achieved in [SCHWARTZ, 100, chap. I] or [BOURBAKI, 16].

Mappings. A mapping T from a set X into a set Y is the data, for each u ∈ X, of an element T(u) ∈ Y. It is said that T is defined on X and that T(u) is the image by T of the point u. The image⁴ by T of a subset U of X is the se...

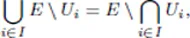
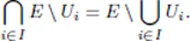
Table of contents

• Cover
• Table of Contents
• Title
• Copyright
• Introduction
• Familiarization with Semi-normed Spaces
• Notations
• Chapter 1: Prerequisites
• PART 1: SEMI-NORMED SPACES
• PART 2: CONTINUOUS MAPPINGS
• PART 3: WEAK TOPOLOGIES
• PART 4: DIFFERENTIAL CALCULUS
• Bibliography
• Cited Authors
• Index
• End User License Agreement