Computational Design of Lightweight Structures

Form Finding and Optimization

Benoit Descamps

• Publisher: Wiley-ISTE
• Year: 2014
• Print ISBN: 9781848216747
• eBook ISBN: 9781118908822
• Edition: 1
• Topic: Mathematics
• Subtopic: Mathematical Analysis
• Index: Mathematics

The author of this book presents a general, robust, and easy-to-use method that can handle many design parameters efficiently.

Following an introduction, Chapter 1 presents the general concepts of truss layout optimization, starting from topology optimization where structural component sizes and system connectivity are simultaneously optimized. To fully realize the potential of truss layout optimization for the design of lightweight structures, the consideration of geometrical variables is then introduced.

Chapter 2 addresses truss geometry and topology optimization by combining mathematical programming and structural mechanics: the structural properties of the optimal solution are used for devising the novel formulation. To avoid singularities arising in optimal configurations, this approach disaggregates the equilibrium equations and fully integrates their basic elements within the optimization formulation. The resulting tool incorporates elastic and plastic design, stress and displacement constraints, as well as self-weight and multiple loading. The inherent slenderness of lightweight structures requires the study of stability issues.

As a remedy, Chapter 3 proposes a conceptually simple but efficient method to include local and nodal stability constraints in the formulation. Several numerical examples illustrate the impact of stability considerations on the optimal design.

Finally, the investigation on realistic design problems in Chapter 4 confirms the practical applicability of the proposed method. It is shown how we can generate a range of optimal designs by varying design settings.

1

Truss Layout Optimization

This chapter presents the general problem of truss layout optimization. After a brief introduction to the standard theory of mathematical programming in section 1.1, section 1.2 derives the governing equations of truss structures. Then, section 1.3 states the basic problem of topology optimization. The equivalence between volume and compliance minimization problems is also studied by means of the necessary conditions of optimality. On this basis, section 1.4 progressively builds up a general formulation by adding different design settings. At each step, the numerical difficulties associated with these building blocks are explained. Finally, the optimization of nodal positions is considered in section 1.5, leading to the general design problem of truss geometry and topology optimization, which remains unsolved in the literature.

1.1. Standard theory of mathematical programming

Consider a general nonlinear optimization problem consisting of the minimization of an objective function subject to inequality and equality constraints [MOR 03]:

[1.1a]

[1.1b]

[1.1c]

where f :

are smooth functions and z ∈

^N_z is a vector of continuous variables. Smoothness of the objective function and the constraints is important to allow for a good prediction of the search direction by optimization algorithms. The feasible set of the optimization problem [1.1] is defined as:

[1.2]

In the feasible region, the inequality constraint g_i (z) ≤ 0 is said to be active if g_i (z) = 0 and inactive if g_i (z) < 0. To solve problem [1.1], we first transform it into an unconstrained optimization problem by introducing Lagrange multipliers

such that:

[1.3]

Thus, solving problem [1.1] amounts now to finding a stationary point to [1.3]. If g_i (z) is active, we ensure that the search direction points toward the feasible region by enforcing the dual feasibility λ_g,i ≥ 0. If g_i is inactive, we can remove the constraint by setting the complementary slackness λ_g,igi (z) = 0. These additional constraints are parts of the Karush–Kuhn–Tucker (KKT) optimality conditions [MOR 03]. Let z* be a local minimizer of problem [1.1]. Provided that some regularity conditions hold, then there exists λ_g,i and λ_h,j such that the first-order necessary conditions of optimality, or KKT conditions, are satisfied:

[1.4a]

[1.4b]

[1.4c]

The regularity conditions or constraint qualifications of problem [1.1] are necessary conditions that enable a numerical treatment by standard algorithms of mathematical programming. There are many constraint qualifications in the literature (see [PET 73] for a comprehensive survey). Hereafter, the following three prominent conditions are listed:

– the linear constraint qualification implies that if g_i and h_j are affine functions, then all subsequent constraint qualifications are satisfied;

– the linear-independence constraint qualification holds if the gradients of active inequality constraints ∇g_i (z*) and equality constraints ∇h_j (z*) are linearly independent at z*;

– the Mangasarian–Fromovitz constraint qualification holds if the gradients of active inequality constraints ∇g_i (z*) and equality constraints ∇h_j (z*) are positive linearly independent at z*.

For the remainder, the special case of linear programming should be mentioned. Such an optimization problem minimizes a linear objective function subject to linear equality and inequality constraints with non-negative variables. The convexity of the problem implies that a local optimum is also a global optimum and authorizes an efficient treatment by optimization algorithms [ALE 01]. We will see in section 1.3 that, very often, it is possible to reformulate topology optimization problems so that linear programming applies.

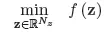
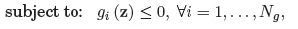
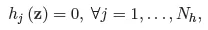
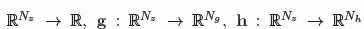
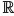
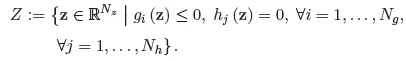
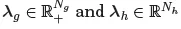
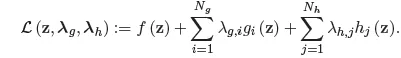
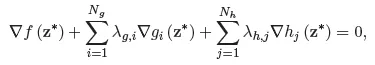
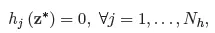
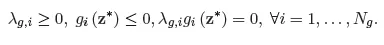
1.2. Governing equations of truss structures

Before stating the structural optimization problem, let us start with some basic notations for a linear elastic truss structure as depicted in Figure 1.1. Using standard finite element concepts, we consider a pin-jointed structure composed of N_n nodes interconnected by truss elements e ∈ {1,…, N_b}. With d ∈ {2, 3} being the spatial dimension and N_s being the number of support reactions, the number of degrees of freedom is N_d = d.N_n – N_s. The vector of nodal coordinates is denoted by x ∈

^d.N_n, the vector of nodal displacements is denoted by u ∈

^N_d and the vector of external forces is denoted by f ∈

^N_d (excluding support reactions). The member force is t_e ∈

. The design parameters associated with every truss element are the...

Table of contents

• Cover
• Table of Contents
• Title Page
• Copyright
• Preface
• Introduction
• 1 Truss Layout Optimization
• 2 Unified Formulation
• 3 Stability Considerations
• 4 Structural Design Applications
• Conclusions and Future Prospects
• Appendix
• Bibliography
• Index