Fat-Tailed Distributions

Data, Diagnostics and Dependence

Roger M. Cooke, Daan Nieboer, Jolanta Misiewicz

• Publisher: Wiley-ISTE
• Year: 2014
• Print ISBN: 9781848217928
• eBook ISBN: 9781119054122
• Edition: 1
• Topic: Mathematics
• Subtopic: Mathematics General
• Index: Mathematics

This title is written for the numerate nonspecialist, and hopes to serve three purposes. First it gathers mathematical material from diverse but related fields of order statistics, records, extreme value theory, majorization, regular variation and subexponentiality. All of these are relevant for understanding fat tails, but they are not, to our knowledge, brought together in a single source for the target readership. Proofs that give insight are included, but for most fussy calculations the reader is referred to the excellent sources referenced in the text. Multivariate extremes are not treated. This allows us to present material spread over hundreds of pages in specialist texts in twenty pages. Chapter 5 develops new material on heavy tail diagnostics and gives more mathematical detail. Since variances and covariances may not exist for heavy tailed joint distributions, Chapter 6 reviews dependence concepts for certain classes of heavy tailed joint distributions, with a view to regressing heavy tailed variables.

Second, it presents a new measure of obesity. The most popular definitions in terms of regular variation and subexponentiality invoke putative properties that hold at infinity, and this complicates any empirical estimate. Each definition captures some but not all of the intuitions associated with tail heaviness. Chapter 5 studies two candidate indices of tail heaviness based on the tendency of the mean excess plot to collapse as data are aggregated. The probability that the largest value is more than twice the second largest has intuitive appeal but its estimator has very poor accuracy. The Obesity index is defined for a positive random variable X as:

Ob(X) = P (X1 +X4 > X2 +X3|X1 ? X2 ? X3 ? X4), Xi independent copies of X.

For empirical distributions, obesity is defined by bootstrapping. This index reasonably captures intuitions of tail heaviness. Among its properties, if ? > 1 then Ob(X) < Ob(X?). However, it does not completely mimic the tail index of regularly varying distributions, or the extreme value index. A Weibull distribution with shape 1/4 is more obese than a Pareto distribution with tail index 1, even though this Pareto has infinite mean and the Weibull's moments are all finite. Chapter 5 explores properties of the Obesity index.

Third and most important, we hope to convince the reader that fat tail phenomena pose real problems; they are really out there and they seriously challenge our usual ways of thinking about historical averages, outliers, trends, regression coefficients and confidence bounds among many other things. Data on flood insurance claims, crop loss claims, hospital discharge bills, precipitation and damages and fatalities from natural catastrophes drive this point home. While most fat tailed distributions are "bad", research in fat tails is one distribution whose tail will hopefully get fatter.

1

Fatness of Tail

1.1. Fat tail heuristics

Suppose the tallest person you have ever seen was 2 m (6 ft 8 in). Someday you may meet a taller person; how tall do you think that person will be, 2.1 m (7 ft)? What is the probability that the first person you meet taller than 2 m will be more than twice as tall, 13 ft 4 in? Surely, that probability is infinitesimal. The tallest person in the world, Bao Xishun of Inner Mongolia, China, is 2.36 m (or 7 ft 9 in). Before 2005, the most costly Hurricane in the US was Hurricane Andrew (1992) at 41.5 billion USD (2011). Hurricane Katrina was the next record hurricane, weighing in at 91 billion USD (2011)¹. People’s height is a “thin-tailed” distribution, whereas hurricane damage is “fat-tailed” or “heavy-tailed”. The ways in which we reason based on historical data and the ways we think about the future are, or should be, very different depending on whether we are dealing with thin- or fat-tailed phenomena. This book provides an intuitive introduction to fat-tailed phenomena, followed by a rigorous mathematical overview of many of these intuitive features. A major goal is to provide a definition of obesity that applies equally to finite data sets and to parametric distribution functions.

Fat tails have entered popular discourse largely due to Nassim Taleb’s book The Black Swan: The Impact of the Highly Improbable ([TAL 07]). The black swan is the paradigm shattering, game-changing incursion from “Extremistan”, which confounds the unsuspecting public, the experts and especially the professional statisticians, all of whom inhabit “Mediocristan”.

Mathematicians have used at least three central definitions for tail obesity. Older texts sometime speak of “leptokurtic distributions”: distributions whose extreme values are “more probable than normal”. These are distributions with kurtosis greater than zero², and whose tails go to zero slower than the normal distribution.

Another definition is based on the theory of regularly varying functions and it characterizes the rate at which the probability of values greater than x go to zero as x → ∞. For a large class of distributions, this rate is polynomial. Unless indicated otherwise, we will always consider non-negative random variables. Letting F denote the distribution function of random variable X, such that

, we write

to mean

is called the survivor function of X. A survivor function with polynomial decay rate –α, or, as we will say, tail index α, has infinite kth moments for all k > α. The Pareto distribution is a special case of a regularly varying distribution where

. In many cases, like the Pareto distribution, the kth moments are infinite for all k ≥ α. Chapter 4 unravels these issues, and shows distributions for which all moments are infinite. If we are “sufficiently close” to infinity to estimate the tail indices of two distributions, then we can meaningfully compare their tail heaviness by comparing their tail indices, such that many intuitive features of fat-tailed phenomena fall neatly into place.

A third definition is based on the idea that the sum of independent copies X₁ + X₂ + … + X_n behaves like the maximum of X₁, X₂,… X_n. Distributions satisfying

are called subexponential. Like regular variation, subexponentiality is a phenomenon that is defined in terms of limiting behavior as the underlying variable goes to infinity. Unlike regular variation, there is no such thing as an “index of subexponentiality” that would tell us whether one distribution is “more subexponential” than another. The set of regularly varying distributions is a strict subclass of the set of subexponential distributions. Other more novel definitions are given in Chapter 4.

There is a swarm of intuitive notions regarding heavytailed phenomena that are captured to varying degrees in the different formal definitions. The main intuitions are as follows:

– the historical averages are unreliable for prediction;

– differences between successively larger observations increases;

– the ratio of successive record values does not decrease;

– the expected excess above a threshold, given that the threshold is exceeded, increases as the threshold increases;

– the uncertainty in the average of n independent variables does not converge to a normal with vanishing spread as n → ∞; rather, the average is similar to the original variables;

– regression coefficients which putatively explain heavy-tailed variables in terms of covariates may behave erratically.

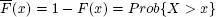
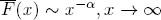
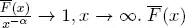
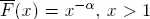
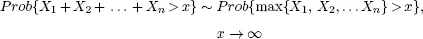
1.2. History and data

A detailed history of fat-tailed distributions is found in [MAN 08]. Mandelbrot himself introduced fat tails into finance by showing that the change in cotton prices was heavy-tailed [MAN 63]. Since then many other examples of heavy-tailed distributions have been found, among these we find data file traffic on the Internet [CRO 97], financial market returns [RAC 03, EMB 97] and magnitudes of earthquakes and floods [LAT 08, MAL 06], to name a few.³

Data for this book were developed in the NSF project 0960865, and are available at http://www.rff.org/Events/Pages/Introduction-Climate-Change-Extreme-Events.aspx, or at public sites indicated below.

1.2.1. US flood insurance claims

US flood insurance claims data from the National Flood Insurance Program (NFIP) are compiled by state and year for the years 1980–2008; the data are in US dollars. Over this time period, there has been substantial growth in exposure to flood risk, particularly in coastal states. To remove the effect of growing exposure, the claims are divided by personal income estimates per state per year from the Bureau of Economic Accounts (BEA). Thus, we study flood claims per dollar income by state and year⁴.

1.2.2. US crop loss

US crop insurance indemnities paid from the US Department of Agriculture’s Risk Management Agency are compiled by state and year for the years 1980–2008; the data are in US dollars. The crop loss claims are not exposure adjusted, since a proxy for exposure is not easy to establish, and exposure growth is less of a concern⁵.

1.2.3. US damages and fatalities from natural disasters

The SHELDUS database, maintained by the Hazards and Vulnerability Research Group at the University of South Carolina, registers states-level damages and fatalities from weather events⁶. The basal estimates in SHELDUS are indications as the approach to compiling the data always employs the most conservative estimates. Moreover, when a disaster affects many states, the total damages and fatalities are apportioned equally over the affected states regardless of population or infrastructure. These data should therefore be seen as indicative rather than precise.

1.2.4. US hospital discharge bills

Billing data for hospital discharges in a northeast US states were collected over the years 2000–2008; the data are in US dollars.

1.2.5. G-Econ data

This uses the G-Econ database [NOR 06] showing the dependence of gross cell product (GCP) on geographic variables measured on a spatial scale of 1°. At 45° latitude, a 1° by 1° grid cell is [45 mi² or [68 km]². The size varies substantially from equator to pole. The population per grid cell varies from 0.31411 to 26,443,000. The GCP is for 1990, non-mineral, 1995 USD, converted at market exchange rates. It varies from 0.000103 to 1,155,800 USD (1995), the units are $10⁶. The GCP per person varies from 0.00000354 to 0.905, which scales from $3.54 to $905,000. There are 27,445 grid cells. Thro...

Table of contents

• Cover
• Contents
• Title Page
• Copyright
• Introduction
• 1 Fatness Of Tail
• 2 Fundamental Parameters of Antennas
• 3 Records
• 4 Regularly Varying and Subexponential Distributions
• 5 Indices and Diagnostics Of Tail Heaviness
• 6 Dependence
• Conclusions and Perspectives
• Bibliography
• Index