Recurrent Event Modeling Based on the Yule Process

Application to Water Network Asset Management

Yves Le Gat

• Publisher: Wiley-ISTE
• Year: 2015
• Print ISBN: 9781848218918
• eBook ISBN: 9781119261322
• Edition: 1
• Topic: Mathematics
• Subtopic: Mathematical Analysis
• Index: Mathematics

This book presents research work into the reliability of drinking water pipes.

The infrastructure of water pipes is susceptible to routine failures, namely leakage or breakage, which occur in an aggregative manner in pipeline networks. Creating strategies for infrastructure asset management requires accurate modeling tools and first-hand experience of what repeated failures can mean in terms of socio-economic and environmental consequences.

Devoted to the counting process framework when dealing with this issue, the author presents preliminary basic concepts, particularly the process intensity, as well as basic tools (classical distributions and processes).

The introductory material precedes the discussion of several constructs, namely the non-homogeneous birth process, and further as a special case, the linearly extended Yule process (LEYP), and its adaptation to account for selective survival. The practical usefulness of the theoretical results is illustrated with actual water pipe failure data.

1
Introduction

Examples of recurrent failures abound in the literature devoted to the reliability of technical objects, and in many cases, the occurrence rates tend to increase not only with the ageing of the object, but also with the number of past failures. The effect of ageing can be relevantly modeled using the now classical non-homogeneous Poisson process (NHPP), a comprehensive presentation of which can be found in [LAW 87], and a good example of application to drinking water pipe failures in [R∅S 00]. In this same context of pipe failures, the PhD work of [EIS 94] emphasizes the critical importance of past failures. The consideration of the dependency of the failure process on its past is not a trivial question, and motivates a theoretical effort which the present book attempts to contribute to.

The basic concept of a stochastic process underlies all developments of the present work. A stochastic process must be understood as a function X() of time t, each X(t) being considered as a random variable (r.v.).

The stochastic process theory is the natural mathematical framework for studying the repetition of random events of the same kind. As presented by [COO 02], this question can be addressed from two alternative perspectives, which are equivalent and respectively consist of modeling:

• – either the distribution of successive inter-arrival times;
• – or the distribution of the number of events that occur in a given time interval.

The method chosen by [EIS 94] arises from the first approach. The “classical” presentation of [ROS 83] arises from the second approach. The linear extension of the Yule process (called LEYP throughout the rest of the book) aims at building a failure occurrence model that cumulates the advantages of both NHPP and [EIS 94]’s approaches. This involves a theoretical setup, focused on the counting process concept, which is to be developed throughout the next two chapters.

A counting process is a particular stochastic process, simply designed to count repeated events, as presented in section 1.2.1.

As this presentation is to have a general scope, the entity subjected to repeated failures will be called a technical object or more simply an object; this term will be replaced by “water main” or “water pipe” when the context refers more specifically to failures that affect a water network.

1.1Notation

The following mathematical notations will be used throughout this book:

• –
  
  and
  
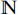  ^* respectively denote the sets of natural integers {0,1,2,…, ∞} and the set of strictly positive natural integers {1,2,…, ∞};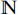
• –
  
  ,
  
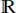  ₊ and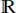
  
  are the real sets ] − ∞, +∞[, [0, +∞[ and ]0, +∞[;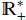
• – P (A) and P (A | B) respectively denote the probability of the event A, and the conditional probability of A given that the other event B occurs;
• – P (A ∩ B) and P (A, B) equivalently denote the joint probability of events A and B ;P (∩_j A_j) more generally stands for the joint probability of events A_j;
• – t ∈
  
  ₊ is a positive time variable...

Table of contents

• Cover
• Table of Contents
• Title
• Copyright
• Preface
• 1 Introduction
• 2 Preliminaries
• 3 Non-homogeneous Birth Process
• 4 Linear Extension of the Yule Process
• 5 LEYP Likelihood and Inference
• 6 Selective Survival
• 7 LEYP2s Likelihood and Inference
• 8 Case Study Application of the LEYP2s Model
• 9 Conclusion and Outlook
• Appendices
• Bibliography
• Index