Graph-related Optimization and Decision Support Systems

Saoussen Krichen, Jouhaina Chaouachi

• Publisher: Wiley-ISTE
• Year: 2014
• Print ISBN: 9781848217430
• eBook ISBN: 9781118984246
• Edition: 1
• Topic: Computer Science
• Subtopic: Information Technology
• Index: Computer Science

Constrained optimization is a challenging branch of operations research that aims to create a model which has a wide range of applications in the supply chain, telecommunications and medical fields. As the problem structure is split into two main components, the objective is to accomplish the feasible set framed by the system constraints. The aim of this book is expose optimization problems that can be expressed as graphs, by detailing, for each studied problem, the set of nodes and the set of edges. This graph modeling is an incentive for designing a platform that integrates all optimization components in order to output the best solution regarding the parameters' tuning. The authors propose in their analysis, for optimization problems, to provide their graphical modeling and mathematical formulation and expose some of their variants. As a solution approaches, an optimizer can be the most promising direction for limited-size instances. For large problem instances, approximate algorithms are the most appropriate way for generating high quality solutions. The authors thus propose, for each studied problem, a greedy algorithm as a problem-specific heuristic and a genetic algorithm as a metaheuristic.

1

Basic Concepts in Optimization and Graph Theory

1.1. Introduction

An optimization problem is a formal specification of a set of proposals related to a specific framework that includes one or numerous decision makers, one or several objectives to be achieved and a set of structural constraints. Optimization has been practiced in numerous fields of study as it provides a primary tool for modeling and solving complex and hard constrained problems. After the 1960s, integer programming formulations and approximate approaches have received considerable attention as useful tools for solving optimization problems. Depending on the problem structure and its complexity, appropriate solution approaches were proposed to generate appropriate solutions in a reasonable computation time. Several optimization studies are formulated as a problem whose goal is to find the best solution, which corresponds to the minimum or maximum value of a single-objective function. The challenge of solving combinatorial problems lies in their computational complexity since most of them are non-deterministic polynomial-time (NP)-hard [GAR 79]. This complexity can mainly be expressed in terms of the relationship between the search space and the difficulty of finding a solution. The search space in combinatorial optimization problems is discrete and multidimensional. The higher the dimensionality, the larger the search space, and the harder the problem. The remainder of this chapter is organized as follows. In section 1.2, we highlight the terminology adopted throughout this book. Section 1.3 deals with the mathematical structure of an optimization problem and enumerates its main variants. Section 1.4 illustrates the previously announced principles by a didactic example. Section 1.5 outlines the main features of an optimization problem.

1.2. Notation

We present in the following the major symbols used for defining an optimization problem:

Symbols	Description
n	the number of decision variables
k	the number of objectives
x = (x1,...,xn)^T	the vector of decision variables
^c(p,n)	the cost matrix
A	the matrix of constraints
B	Resources limitations
EO	The set of efficient solutions in the objective space
ED	The set of efficient solutions in the decision space

1.3. Problem structure and variants

Assuming the linearity of an optimization problem, its mathematical modeling is outlined as follows:

[1.1]

[1.2]

[1.3]

where x = (x₁,…,x_n)^T denotes the vector of decision variables, p, b and A are constant vectors and matrix of coefficients, respectively.

Many variants of this formulation can be pointed out:

– Continuous linear programming (CLP): The optimization model [1.1]-[1.3] is a CLP if the decision variables are continuous. For continuous linear optimization problems, efficient exact algorithms such as the simplex-type method [BUR 12] or interior point methods exist [ANS 12].

– Integer linear programming (ILP): The optimization model [1.1]-[1.3] is an ILP if χ is the set of feasible integer solutions (i.e. decision variables are discrete). This class of models is very important as many real-life applications are modeled with discrete variables since their handled resources are indivisible (as cars, machines and containers). A large number of combinatorial optimization problems can be formulated as ILPs (e.g. packing problems, scheduling problems and traveling salesman) in which the decision variables are discrete and the search space is finite. However, the objective function and constraints may take any form [PAP 82].

– Mixed integer programming (MIP): The optimization model [1.1]-[1.4] is called MIP, when the decision variables are both discrete and continuous. Consequently, MIP models generalize the CLP and ILP models. MIP problems have improved dramatically of late with the use of advanced optimization techniques such as relaxations and decomposition approaches, branch-and-bound, and cutting plane algorithms when the problem sizes are small [GAR 12, WAN 13, COO 11]. Metaheuristics are also a good candidate for larger instances. They can also be used to generate good lower or upper bounds for exact algorithms and improve their efficiency.

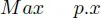
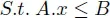
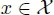
1.4. Features of an optimization problem

Optimization problems can be classified in terms of the nature of the objective function and the nature of the constraints. Special forms of the objective function and the constraints give rise to specialized models that can efficiently model the problem under study. From this point of view, various types of optimization models...

Table of contents

• Cover
• Contents
• Title Page
• Copyright
• List of Tables
• List of Figures
• List of Algorithms
• Introduction
• 1 Basic Concepts in Optimization and Graph Theory
• 2 Knapsack Problems
• 3 Packing Problems
• 4 Assignment Problem
• 5 The Resource Constrained Project Scheduling Problem
• 6 Spanning Tree Problems
• 7 Steiner Problems
• 8 A DSS Design for Optimization Problems
• Conclusion
• Glossary
• Bibliography
• Index