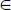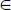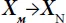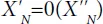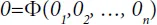Hydraulic Modeling

Victor M. Lyatkher, Alexander M. Proudovsky

• Publisher: Wiley-Scrivener
• Year: 2016
• Print ISBN: 9781118946190
• eBook ISBN: 9781118946206
• Edition: 1
• Topic: Politics & International Relations
• Subtopic: Environment & Energy Policy
• Index: Politics & International Relations

Water. Except for air, it is the most important ingredient to all life on Earth. It surrounds us every day. We are literally bathed in it, we cook our food with it, and we need a steady stream of it in our bodies every single day just to survive. But water, and the study of it, is one of the most important and unheralded branches of engineering, affecting every other aspect of engineering in almost every industry. We harness its power for energy, we inject massive blasts of it into the earth to extract oil, gas, and minerals, and we use it in nearly every single industrial application, including food processing, refining, manufacturing, and waste disposal, just to name a few.

Hyraulic modeling is, essentially, the understanding and prediction of fluid flow and its applications in industrial, municipal, and environmental settings, whether in a creekbed, locked in the pores of rocks deep in the earth, or in the ocean. Mathematical models, which started out with mechanical pencils and drafting tables originally, have been increasingly relied upon over the last few decades, due to the invention, growth, and refinement of computers. Physical modeling, however, is still practiced in laboratories, and it is the intersection of physical and mathematical modeling of fluid flow that is most successful in creating models that are safer, less costly, and are better for the environment.

Hydraulic Modeling introduces and explores this incredibly important science, from the most basic tenets to valuable real-world applications that are used in industry today. It is the only volume on the market to offer a thorough coverage of the subject without adding lots of useless fluff or inapplicable appendices. It is a must-have for any engineer, scientist, or student working with hydraulic modeling, as a daily reference or a textbook.

Chapter 1

Fundamentals of Modeling

1.1 Modeling as the Method of Cognition

Modeling is one of the most important ways of cognition. When using this method the object of cognition (the original, nature, prototype) is realized through studying of its substitute, which is called the model. If the nature of N is characterized by a number of X_N

N, values, then when modeling such an object M is created, the characteristics X_M

M of which are determined according to the nature values:

The term “model” in the theory of knowledge is rather ambiguous, making classifying models complicated. For our purposes it is important to divide models as substantive and symbolic. The first of them are material objects, whose characteristics are somehow corresponding to the characteristics of the nature. The second represent notation symbols (diagrams, graphs, drawings, formulas, words, and so on). The most important type of symbolic models are the mathematical (logical-mathematical) models, realized by the means of mathematical language and logic.

Mathematical models of fluid flows include continuity equations, conservation of momentum equations, energy conservation and condition equations in one or another form. For multiphase fluids the equations are written for each phase with the inclusion of terms that characterize the interaction of phases. The equations contain some schematization of hydraulic phenomena. The quality of mathematical models depends on how successful the schematization is: some models can be better than others, but they all have some degree of uncertainty and inaccuracies, as they are based on a hypothesis. Quality assessment of a mathematical model (relevancy of underlying hypotheses) is the comparison of values, corresponding to the hypothesis used, with the measured characteristics of the real phenomena to which they relate. Of course, there are new challenges associated with the estimation of accuracy of measurement results, which usually cannot be executed without using the model of the phenomenon. Thus, the problem of estimation of the model is very complicated in principle.

Formulation of the mathematical model does not exhaust the modeling process. To predict the phenomenon it is necessary to establish a correspondence between the values X″_N, characterizing the problem specification and values of X′_N, forming its solution. Such a correspondence is set up by a certain operator O:

(1.1)

The operation O is executed using different computational tools. The way of realization of the operator is the main characteristic for classification of modeling in engineering. On this basis it is possible to allocate the first two large classes.

Modeling of the first class combines the cases in which the operator is represented in the form of an assistant operators function:

(1.2)

The solution is resulted from consecutive impact of operators from the set {O_i} on basic values and the intermediate results according to plan, designed in accordance with the type of the Φ function. In this case we speak of a computational process. The order of operations, providing representation of the source data in the solution of this problem is called the algorithm of its solution. Modeling, using computational process can be called numerical modeling.

The principal place among computing devices, used in modeling and belonging to this class, is occupied by digital electronic computing machines (computers). It is easy to notice that the operations carried out by a computer at “manual” solving of the physical problem, are a particular case of numerical modeling.

The second class modeling uses methods and tools, implying the direct, carried out in one time representation of quantities included in the problem specification, its solution. These means include analog devices, and each of them represents a physical model of a particular class of mathematical problems. This model allows carrying out direct measurement of the considered characteristics, corresponding to these or that basic values. Modeling using analog means is called analog modeling.

The process of analog modeling of a phenomenon can be described by the following scheme:

phenomenon (nature) ->mathematical model (system of mathematical equations) ->
physical model (analog medium) -> - nature

The physical model included in this scheme is commonly called the phenomenon model. It is clear that this phenomenon model corresponds to the studied phenomenon so its mathematical model is accurate.

Thus, in case of analog modeling, the physical model and nature are related through formally similar mathematical model. Here phenomena in kind and on the model may have different physical nature in general case. The fact that various phenomena have the same mathematical description is not associated with the random formal analogy of the mathematical apparatus. It is concerned with the unity of regularities of processes of different kinds of material motion.

The models representing the phenomenon of the same kind show characteristics which you want to predict, and constitute the special type of analog means. With the understanding that further such analog devices shall be called physical models, unlike the analogs in those cases, the nature and the model represent heterogeneous phenomena.

The main difference of the physical model and the analogous is that the physical model’s natural characteristics correspond to the homogeneous (one-nominal) characteristics (speed - the speed, pressure-pressure, etc.), and the analog portion of them (or all) can comply with heterogeneous characteristics. In this sense, the flow of fluid may be physical model (routine hydraulic and aerodynamic modeling) and analog (gas hydraulic, gravity-elastic analogy).

A physical model of the hydraulic phenomenon is usually called a hydraulic model and the modeling with the use of such models – hydraulic modeling. This definition is inaccurate, as any hydraulic modeling phenomena refers to hydraulics and can be called hydraulic. Here, however, the author decided not to break the tradition and, moreover, this term in the title of the book.

1.2 Hydraulic and Numerical Modeling

Hydraulic and numerical modeling of hydraulic phenomena shall be compared now. If hydraulic modeling is a traditional method of hydraulic engineering, successfully used in the last century, numerical modeling with the use of computers - is the latest achievement. The range of problems solved by means of numerical modeling is constantly expanding. It opens new perspectives in solving complex hydraulic problems. Optimal for the development of applied hydromechanics is to use the advantages of hydraulic and numerical modeling in combination.

Between hydraulic and numerical modeling has a great community, namely, that, first, they are based on a mathematical model of the phenomenon, reflecting the most significant side of the studied object, and, secondly, when modeling the object significantly schematized. Differences in hydraulic and numerical modeling can be caused by the following circumstances. Hydraulic model is a highly specialized tool, while computers can be a solution for the most diverse problems. The only condition is the possibility of receiving the decision, in their algorithmic solvability of a problem on the selected set of operators {O_i}. Modern computers have successful from this point of view, the set of elementary operators.

The main advantage of hydraulic models is that with their help it is possible to find the solution of problems even in cases where the mathematical model of the phenomenon are not complete and take advantage of the numerical modeling impossible. As is known, up to now there is not a closed system of equations describing the averaged velocity field and pressure turbulent flow. However, if we assume that these equations have the same form for nature and models, it is possible to determine the conditions of conversion of measurement results on models in nature (see Section 1.3).

Another advantage of hydraulic models is the relative simplicity of the complex conditions of the solution uniqueness. Uniqueness conditions (first of all the geometric shape of the boundaries) for natural flows are especially complicated. To set the channel form on a computer, you need to put into it a lot of figures characterizing at least from the bottom to the length and width of the stream. In addition, you need to enter the operation of the “smooth...

Table of contents

• Cover
• Half Title page
• Title page
• Copyright page
• Dedication
• Introduction
• Chapter 1: Fundamentals of Modeling
• Chapter 2: The Mathematical Models of Fluid Motion
• Chapter 3: Approximate Similarity of Hydraulic Phenomenon
• Chapter 4: Pressure Flows
• Chapter 5: Open Flow in Hard Channel
• Chapter 6: Multi-Component Flows
• Chapter 7: Flow in the Deformable Channel
• Chapter 8: Heat and Mass Transfer and Phase Transitions
• Chapter 9: Hydrodynamic Loads
• Conclusion
• References
• Appendix
• Index