Growth Curve Modeling

Theory and Applications

Michael J. Panik

• Publisher: Wiley
• Year: 2014
• Print ISBN: 9781118764046
• eBook ISBN: 9781118763940
• Edition: 1
• Topic: Mathematics
• Subtopic: Business Development
• Index: Mathematics

Features recent trends and advances in the theory and techniques used to accurately measure and model growth

Growth Curve Modeling: Theory and Applications features an accessible introduction to growth curve modeling and addresses how to monitor the change in variables over time since there is no "one size fits all" approach to growth measurement. A review of the requisite mathematics for growth modeling and the statistical techniques needed for estimating growth models are provided, and an overview of popular growth curves, such as linear, logarithmic, reciprocal, logistic, Gompertz, Weibull, negative exponential, and log-logistic, among others, is included.

In addition, the book discusses key application areas including economic, plant, population, forest, and firm growth and is suitable as a resource for assessing recent growth modeling trends in the medical field. SAS® is utilized throughout to analyze and model growth curves, aiding readers in estimating specialized growth rates and curves. Including derivations of virtually all of the major growth curves and models, Growth Curve Modeling: Theory and Applications also features:

• Statistical distribution analysis as it pertains to growth modeling
• Trend estimations
• Dynamic site equations obtained from growth models
• Nonlinear regression
• Yield-density curves
• Nonlinear mixed effects models for repeated measurements data

Growth Curve Modeling: Theory and Applications is an excellent resource for statisticians, public health analysts, biologists, botanists, economists, and demographers who require a modern review of statistical methods for modeling growth curves and analyzing longitudinal data. The book is also useful for upper-undergraduate and graduate courses on growth modeling.

1

MATHEMATICAL PRELIMINARIES

1.1 ARITHMETIC PROGRESSION

We may define an arithmetic progression as a set of numbers in which each one after the first is obtained from the preceding one by adding a fixed number called the common difference. Suppose we denote the common difference of an arithmetic progression by d, the first term by a₁, …, and the nth term by a_n. Then the terms up to and including the nth term can be written as

(1.1)

If S_n denotes the sum of the first n terms of an arithmetic progression, then

(1.2)

If the n terms on the right-hand side of Equation 1.2 are written in reverse order, then S_n can also be expressed as

(1.3)

Upon adding Equations 1.2 and 1.3, we obtain

or

(1.4)

EXAMPLE 1.1 Given the arithmetic progression –3, 0, 3, …, determine the 50th term and the sum of the first 100 terms. For a₁ = –3, the second term (0) minus the first term is 0 – (–3) = 3 = d, the common difference. Then, from Equation 1.1,

and, from Equation 1.4,

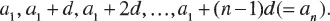
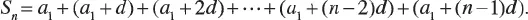
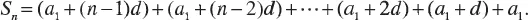
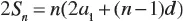
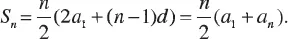
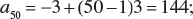
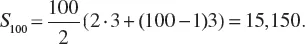
1.2 GEOMETRIC PROGRESSION

A geometric progression is any set of numbers having a common ratio; that is, the quotient of any term (except the first) and the immediately preceding term is the same. Suppose we represent the common ratio of a geometric progression by r, the first term by a₁(≠0), ∆, and the nth term by a_n. Then the terms up to and including the nth term are

(1.5)

(Note that, as required,

If the sum of the first n terms of a geometric progression is denoted as S_n, then

(1.6)

Using Equation 1.6, let us form

(1.7)

so that, upon subtracting Equation 1.7 from Equation 1.6, we obtain

or

(1.8)

EXAMPLE 1.2 Given the geometric progression 1/2, 3/4, 9/8, …, determine the sixth term and the sum of the first nine terms. For a₁ = 1/2, the second term (3/4) divided by the first term (1/2) is (3/4)/(1/2) = 3/2 = r, the common ratio. Then, from Equation 1.5,

and, from Equation 1.8,

Suppose we have a geometric progression with infinitely many terms. The sum of the terms of this type of geometric progression, in which the value of n can increase without bound, is called a geometric series and has the form

(1.9)

If we again designate the sum of the first n terms in Equation 1.9 as S_n (here S_n is called a finite partial sum of the first n terms) or Equation 1.6, then, via Equation 1.8,

(1.10)

If |r| < 1, then the second term in the difference on the right-hand side of Equation 1.10 decreases to zero as n increases indefinitely (rⁿ → 0 as n → ∞). Hence,

(1.11)

Thus, the geometric series S is said to converge to the value a₁/(1 – r). If |r| > 1, the finite partial sums S_n do not approach any limiting value—the geometric series S does not converge; it is said to diverge since |rⁿ| → ∞ as n → ∞.

EXAMPLE 1.3 Given the geometric progression

does the geometric series

converge? If so, to what value? Given r = 1/3, the nth finite partial sum is

and, via Equation 1.10,

Then

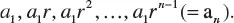
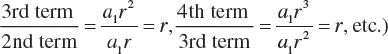
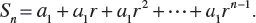
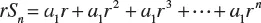
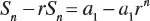
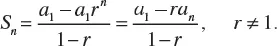
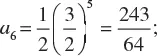
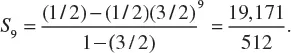
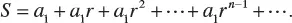
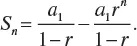
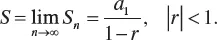
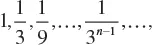
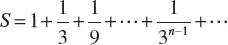
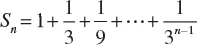
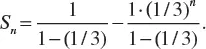
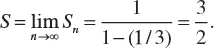
1.3 THE BINOMIAL FORMULA

Suppose we are interested in finding (a + b)ⁿ, where n is a positive integer. According to the binomial formula,

(1.12)

with the coefficients of the terms on the right-hand side of Equation 1.12 termed binomial coefficients corresponding to the exponent n. For instance, from Equation 1.12,

Note that, in general:

1....

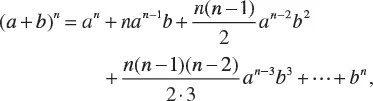
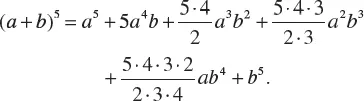
Table of contents

• COVER PAGE
• CONTENTS
• TITLE PAGE
• COPYRIGHT
• DEDICATION
• PREFACE
• 1 MATHEMATICAL PRELIMINARIES
• 2 FUNDAMENTALS OF GROWTH
• 3 PARAMETRIC GROWTH CURVE MODELING
• 4 ESTIMATION OF TREND
• 5 DYNAMIC SITE EQUATIONS OBTAINED FROM GROWTH MODELS
• 6 NONLINEAR REGRESSION
• 7 YIELD–DENSITY CURVES
• 8 NONLINEAR MIXED–EFFECTS MODELS FOR REPEATED MEASUREMENTS DATA
• 9 MODELING THE SIZE AND GROWTH RATE DISTRIBUTIONS OF FIRMS
• 10 FUNDAMENTALS OF POPULATION DYNAMICS
• APPENDIX A
• REFERENCES
• INDEX