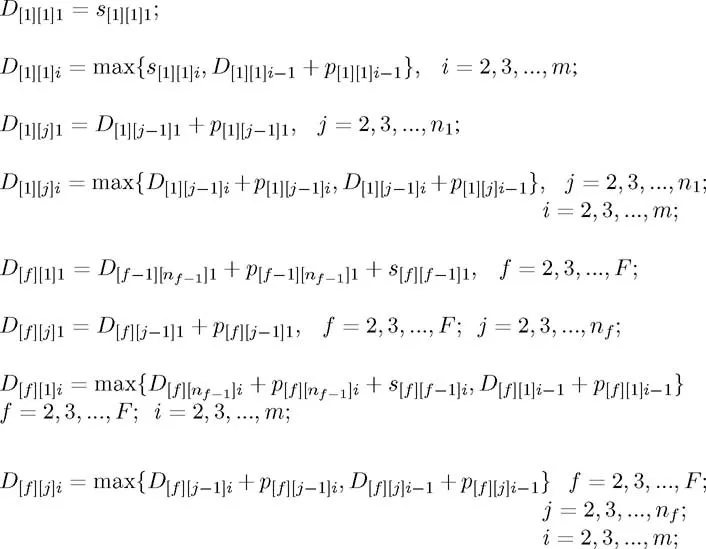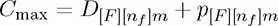Metaheuristics for Production Scheduling

Bassem Jarboui, Patrick Siarry, Jacques Teghem, Bassem Jarboui, Patrick Siarry, Jacques Teghem

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN: 9781848214972
• eBook ISBN: 9781118731567
• Edition: 1
• Topic: Technology & Engineering
• Subtopic: Quality Control in Engineering
• Index: Technology & Engineering

This book describes the potentialities of metaheuristics for solving production scheduling problems and the relationship between these two fields.

For the past several years, there has been an increasing interest in using metaheuristic methods to solve scheduling problems. The main reasons for this are that such problems are generally hard to solve to optimality, as well as the fact that metaheuristics provide very good solutions in a reasonable time. The first part of the book presents eight applications of metaheuristics for solving various mono-objective scheduling problems. The second part is itself split into two, the first section being devoted to five multi-objective problems to which metaheuristics are adapted, while the second tackles various transportation problems related to the organization of production systems.

Many real-world applications are presented by the authors, making this an invaluable resource for researchers and students in engineering, economics, mathematics and computer science.

Chapter 1

An Estimation of Distribution Algorithm for Solving Flow Shop Scheduling Problems with Sequence-dependent Family Setup Times

1.1. Introduction

Since the 1960s, the development of cellular manufacturing systems (CMS) as a technology has drawn the attention of both researchers and manufacturers in the production system industry. Its principal focus is to reduce complexity and improve the output of production lines [GRE 84]. Operationally, the CMS entails arranging a set of similar jobs into part families. Their similarities concern job preparation time, machine requirements and necessary operations.

Several industrial applications can be included in CMS environments, such as the production of microchips, the manufacture of metal products and manual assembly industries [GRE 84]. Hendizadeh et al. [HEN 08] have provided an overview of CMS scheduling problems.

In this chapter, we will focus on a CMS scheduling problem while processing jobs with the same setup family together. Moreover, in each family, there is a set of n jobs that must be executed on a set of m machines following the same order of execution without preemption (no interruption is allowed). Such cells are known as flowline cells or pure flow shop manufacturing cells [SCH 00]. In practice, this problem arises when the scheduling time required for two jobs in the same family is restricted or included in the execution time. This problem occurs when the time required to shift from one part (job) to another is negligible or included in the processing times. However, the time required to shift from one family to another is high and cannot be ignored. Cheng et al. [CHE 00] have provided a comprehensive review for flow shop scheduling problems with setup times. They have classified the problem considered in this chapter in the category of scheduling problems with sequence-dependent family setup times (SDFST). Schaller et al. [SCH 00] have examined a real-world application in the manufacture of printing circuit boards where cell manufacturing systems are strongly required.

Garey and Johnson [GAR 79] have demonstrated that this problem is NP-hard if we minimize the maximum completion time (makespan). This justifies the use of approximate algorithms over exact methods for solving this problem. The use of approximation algorithms is recommended for solving this kind of problem. Schaller et al. [SCH 00] have proposed lower bounds on the makespan criterion in order to introduce them into a branch and bound algorithm. The obtained results have shown that the proposed algorithm appears effective for small-scale instances. Nevertheless, when the number of families or machines increases, the performance of lower bounds drops considerably. In addition, this piece of research also proposed several constructive heuristics. The experimental results for these heuristics have shown that Campbell et al.’s “CDS” heuristic [CAM 70] is the best suited for scheduling jobs in each family. Furthermore, the well-known NEH heuristic [NAW 83] appears to be the most appropriate for family sequencing. França et al. [FRA 05] have examined two evolutionary algorithms (EAs), including a genetic algorithm (GA) and a mimetic algorithm (MA). The results have shown the effectiveness of these two algorithms in relation to the approaches previously described in the literature. In addition, MA shows a slight superiority in relation to GA. Hendizadeh et al. [HEN 08] have employed concepts of the simulated annealing (SA) algorithm to create a balance between intensification and diversification in the search’s direction. The obtained experimental results have shown that the proposed algorithm provides a better quality of solution in relation to Schaller et al.’s [SCH 00] constructive heuristics in terms of solution quality but not in terms of Central Processing Unit (CPU) time. In addition, on average, Tabu Search (TS) and MA algorithms perform similarly. Lin et al. [LIN 09] have proposed three metaheuristics such as SA, GA and TS to solve this problem. It should be noted that SA and GA algorithms perform better than França et al.’s [FRA 05] MA and Hendizadeh et al.’s [HEN 08] TS algorithms, both in terms of the quality of solution and execution time.

In this chapter, we will propose an estimation of distribution algorithm (EDA) for solving a flow shop scheduling problem with SDFST. In addition, an improvement procedure is incorporated into this algorithm in the form of an iterated local search (ILS) algorithm.

The remainder of this chapter is organized as follows. In section 1.2, we will examine a mathematical formulation of the problem. Section 1.3 provides an overview of the literature on EDAs. Section 1.4 will describe the components of the proposed algorithm. The experimental results will be discussed in section 1.5. Finally, section 1.6 provides a conclusion of these results.

1.2. Mathematical formulation

In a flow shop scheduling problem with SDFST, we suppose that each family f (f = 1,2,…, F contains a set of n_f jobs that must be executed on a set of m machines. The job execution order is the same for all machines. In addition, we suppose that the job setup time within each family is included in the execution time. Nevertheless, if a family f immediately follows another family f′ in the sequence of families, the time required between the executions of f and f′ on a machine i (i = 1,2,…,m) is expressed as ^s[f][f′], i. D_f,j,i and pf,j,i are the departure and execution times, respectively, for the job j (j = 1,2,…, n_f) on the machine i in the family f. In the same way, D_[f][j]i and p _[f][j]i express the departure and execution times, respectively, of the job scheduled in the j^th position in the job sequence on the machine i in the f^th family.

The formulation of this problem relies on the following hypotheses [HEN 08]:

– all the jobs are ready for execution at the departure of scheduling (from the date 0);

– the number of jobs and their execution time as well as the number of families and their setup time are positive integers known in advance;

– if the execution of a job in a family begins, it cannot be interrupted by a job from another family.

Given the job sequence in each family and the sequence of all the families, the value of the maximum completion time (makespan) can be obtained using recursive equations, depending on the departure time, as follows:

Therefore:

Based on the three field notation α |β| γ by Graham et al. [GRA 79] to describe a scheduling problem, the field α describes the machine environment. The field β describes the setup data, the other production conditions and the execution characteristics. This field may contain several inputs at the same time. Finally, the field, γ contains the problem’s objective function. As a result, the problem examined in this chapter is denoted by F |ST_sd,b| C_max.

1.3. Estimation of distribution algorithms

In nature, the notion of species’ evolution through sexual reproduction was first formulated by Charles Darwin [BAC 96]. It can be modeled using three mechanisms, such as crossing, mutation and selection. The crossing process occurs as a result of the meiotic combination of two parental chromosomes. As a result of this process, a new individual inherits the different combinations of genes from these parents. Mutation results from errors when copying genetic material during cell division.

EAs are included in a class of algorithms that use computer tools to simulate natural species evolution to solve difficult optimization problems by evolving a population of candidate solutions. EAs have proved their effectiveness in relation to classic optimization techniques [FOG 95]. Several algorithms are included in this class, such as GAs that are more commonly used in the literature.

Recently, Mühlenbein and Paass [MUH 96] have introduced an evolutionary algorithm called Estimation of Distribution Algorithm. As its name implies, this algorithm is based on a probability distribution taken from a population of individuals. Unlike other evolutionary algorithm approaches, EDA uses neither crossover nor mutation. From a population of individuals (candidate solutions), generally generated at random, the EDA selects the good individuals in relation to their fitness. A probability distribution is then estimated from the selected candidates. New offspring are then generated from the estimated distribution. Finally, the process is repeated until a specific stop criterion is satisfied.

Various versions of the EDA have been proposed in the literature that differ according to the constructed probabilistic model. These versions can be classified into three categories: univariate EDAs, where there is no dependence between variables, bivariate EDAs, where interactions between variables are of second order and EDAs with multiple dependencies, also known as multivariate EDAs. The latter category is an amalgamation of the two initial ty...

Table of contents

• Cover
• Table of Contents
• Title Page
• Copyright
• Introduction and Presentation
• Chapter 1: An Estimation of Distribution Algorithm for Solving Flow Shop Scheduling Problems with Sequence-dependent Family Setup Times
• Chapter 2: Genetic Algorithms for Solving Flexible Job Shop Scheduling Problems
• Chapter 3: A Hybrid GRASP-Differential Evolution Algorithm for Solving Flow Shop Scheduling Problems with No-Wait Constraints
• Chapter 4: A Comparison of Local Search Metaheuristics for a Hierarchical Flow Shop Optimization Problem with Time Lags
• Chapter 5: Neutrality in Flow Shop Scheduling Problems: Landscape Structure and Local Search
• Chapter 6: Evolutionary Metaheuristic Based on Genetic Algorithm: Application to Hybrid Flow Shop Problem with Availability Constraints
• Chapter 7: Models and Methods in Graph Coloration for Various Production Problems
• Chapter 8: Mathematical Programming and Heuristics for Scheduling Problems with Early and Tardy Penalties
• Chapter 9: Metaheuristics for Biobjective Flow Shop Scheduling
• Chapter 10: Pareto Solution Strategies for the Industrial Car Sequencing Problem
• Chapter 11: Multi-Objective Metaheuristics for the Joint Scheduling of Production and Maintenance
• Chapter 12: Optimization via a Genetic Algorithm Parametrizing the AHP Method for Multicriteria Workshop Scheduling
• Chapter 13: A Multicriteria Genetic Algorithm for the Resource-constrained Task Scheduling Problem
• Chapter 14: Metaheuristics for the Solution of Vehicle Routing Problems in a Dynamic Context
• Chapter 15: Combination of a Metaheuristic and a Simulation Model for the Scheduling of Resource-constrained Transport Activities
• Chapter 16: Vehicle Routing Problems with Scheduling Constraints
• Chapter 17: Metaheuristics for Job Shop Scheduling with Transportation
• List of Authors
• Index