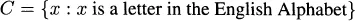The Elements of Cantor Sets

With Applications

Robert W. Vallin

• Publisher: Wiley
• Year: 2013
• ISBN:
  9781118407431
• Edition: 1
• Topic: Mathématiques
• Subtopic: Analyse mathématique

A systematic and integrated approach to Cantor Sets and their applications to various branches of mathematics

The Elements of Cantor Sets: With Applications features a thorough introduction to Cantor Sets and applies these sets as a bridge between real analysis, probability, topology, and algebra.

The author fills a gap in the current literature by providing an introductory and integrated perspective, thereby preparing readers for further study and building a deeper understanding of analysis, topology, set theory, number theory, and algebra.

The Elements of Cantor Sets provides coverage of:

• Basic definitions and background theorems as well as comprehensive mathematical details
• A biography of Georg Ferdinand Ludwig Philipp Cantor, one of the most significant mathematicians of the last century
• Chapter coverage of fractals and self-similar sets, sums of Cantor Sets, the role of Cantor Sets in creating pathological functions, p -adic numbers, and several generalizations of Cantor Sets
• A wide spectrum of topics from measure theory to the Monty Hall Problem

An ideal text for courses in real analysis, topology, algebra, and set theory for undergraduate and graduate-level courses within mathematics, computer science, engineering, and physics departments, The Elements of Cantor Sets is also appropriate as a useful reference for researchers and secondary mathematics education majors.

CHAPTER 1

A QUICK BIOGRAPHY OF CANTOR

Georg Cantor
Library of Congress, courtesy AIP Emilio Segr Visual Archives

Georg Ferdinand Ludwig Philipp Cantor was one of the most important mathematicians of the last half of the 19th century. Born 3 March 1845 in St. Petersburg, Russia, he was the oldest of six children. Due to his father’s ill health, the family moved to Frankfurt, Germany, hoping to find milder winters. In 1862 he started his higher schooling at the Federal Polytechnic Institute in Zürich. After the death of his father, Cantor moved on to study at the University of Berlin. Among his professors there were Kronecker, Weierstrass, and Kummer. In 1867, he earned his PhD for his thesis entitled “De aequationibus secundi gradus indeterminatis (On Indeterminate Equations of the Second Degree).”

Cantor began teaching at the University of Halle, where he would spend his entire career, in 1869. He was promoted to full professor in 1879, which was an achievement at such a young age. However, Cantor wanted to move to the more prestigious University of Berlin, hoping to become chair of the department. This could not happen as Kronecker, who led the department at Berlin, was not supportive of Cantor and his work. Kronecker was one of the founders of the constructive viewpoint; that means only dealing with mathematical objects that could be explicitly made. As an example of Kronecker’s feelings on this, when von Lindemann proved the existence of transcendental numbers (a type of number defined later on in this book), Kronecker praised the proof, but also said the argument [19] “proved nothing because there were no transcendental numbers.” Much of Cantor’s work dealt with sets whose members could be described and were well-defined, but not explicit. Kronecker went so far as to try and pressure Heine to not publish Cantor’s paper “Über trigonometrische Reihen” in the journal Mathematische Annalen. In a letter to Hermite, Cantor complained that Kronecker, among, other things, called his work “humbug.” The pressure from the non-acceptance of his work would drive Cantor into periods of depression, which he suffered from until the end of his life.

He carried on correspondence with some of the greater mathematicians of the day (e.g., Mittag-Leffler, Dedekind), but would at times cease communication. He was very sensitive to even well-intentioned criticisms of his work. In 1894, Cantor suffered his first attack of depression. He even turned his attention away from mathematics for a time, lecturing on philosophy and working on proving that Shakespeare did not write the plays attributed to him. Instead, Cantor believed they were written by Francis Bacon.

Cantor was hospitalized again for depression in 1899 and then several more times starting in 1904. These sapped him of much of his zeal for mathematics. However, his work continued to be appreciated. In 1912 he was awarded an honorary doctorate from the University of St. Andrews in Scotland. He officially retired in 1913 and died on 6 January 1918 in a sanatorium where he had been for the last year of his life.

Cantor’s contributions to mathematics are vast, with results in number theory (his thesis topic) and set theory (which he founded). Some of his most well-known ideas are the Cantor Set, the notion of different types of infinities, and the Continuum Hypothesis. Working on the infinite drew the ire of some mathematicians, philosophers, and religious scholars. Philosophers felt there were too many contradictions in dealing with the infinite. For example, if a and b are two positive numbers, then a < a+b and b < a + b. However, ∞ < a + ∞ is not true. No less a mathematician than Poincare said that in the future people would look on Cantor’s work as “a disease from which one has recovered.” To quote from [19]:

Christian theologians were also opposed to the actual infinite; for the most part they regarded the idea as a direct challenge to the unique and absolutely infinite nature of God.

However, Cantor was not without his supporters. At the Second International Congress held at the Paris World Exposition of 1900, David Hilbert presented a list of the major unsolved problems of the time, hoping to spur interest in what he believed to be the most important problems of the day. The item at the top of the list was Cantor’s Continuum Hypothesis. Hilbert is famously quoted as saying, “No one will drive us from the paradise which Cantor created for us.”

Hubert’s influence was profound, as can be seen in the vast list of papers written just in the last few years that mention Cantor, Cantor Sets, Cantor Measure, Cantor Spaces, and more.

CHAPTER 2

BASICS

This is the “review” chapter. That means much of what we look at here the reader is familiar with. Thus there will not be a lot of proofs given. Most of these concepts are familiar, even if a bit of dust must be shaken off. Hopefully those ideas which are unfamiliar will be few and easily digested by the reader.

2.1 Review

This chapter begins with sets. A set is a well-defined collection of objects. We will use capital letters to denote a set. There are two typical ways to write a set: List Notation and Set-Builder Notation. As the name suggests. List Notation means the writer lists (some of) the objects in the set. Note that sets are written using braces for enclosure. For example, A = {a, b, c, d) or B = {1, 2, 3, …, 9, 10}, where the ellipses (…). means “continue in this manner.” For Set-Builder Notation, rather than listing the items in the set, the members are described by some proposition, P(x). This is a useful way of doing things as some sets defy listing. An example of this notation is

which is of the form {x : P(x)}. The colon is usually translated as “such that” or “so that,” and then followed by a description. This is read as. “C is the set of x such that x is a letter in the English Alphabet.”...